题目内容
1.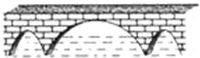 如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为20m,顶点距水面6m,小孔顶点距水面4.5m.当水位上涨刚好淹没小孔时,大孔的水面宽度为10m.
如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为20m,顶点距水面6m,小孔顶点距水面4.5m.当水位上涨刚好淹没小孔时,大孔的水面宽度为10m.
分析 根据题意,建立如图所示的平面直角坐标系,可以得到A、B、M的坐标,设出函数关系式,待定系数求解函数式.根据NC的长度,得出函数的y坐标,代入解析式,即可得出E、F的坐标,进而得出答案.
解答 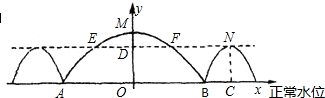 解:如图,建立如图所示的平面直角坐标系,由题意得,M点坐标为(0,6),A点坐标为(-10,0),B点坐标为(10,0),
解:如图,建立如图所示的平面直角坐标系,由题意得,M点坐标为(0,6),A点坐标为(-10,0),B点坐标为(10,0),
设中间大抛物线的函数式为y=-ax2+bx+c,
代入三点的坐标得到$\left\{\begin{array}{l}{c=6}\\{100a-10b+c=0}\\{100a+10b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{3}{50}}\\{b=0}\\{c=6}\end{array}\right.$.
∴函数式为y=-$\frac{3}{50}$x2+6.
∵NC=4.5米,
∴令y=4.5米,
代入解析式得x1=5,x2=-5,
∴可得EF=5-(-5)=10米.
故答案为:10.
点评 本题考查了待定系数法求二次函数的解析式,由函数值求自变量的值的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
11.一元二次方程x2-4x+4=0的根的情况为( )
| A. | 只有一个实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
10.下列图形是中心对称图形的是( )
| A. | 平行四边形 | B. | 直角三角形 | C. | 等边三角形 | D. | 正五边形 |
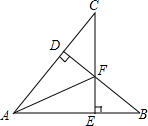 已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线.
已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线. (1)已知:如图,点C在线段AB上,线段AC=12,BC=4,点M、N分别是AC、BC的中点,求MN的长度.
(1)已知:如图,点C在线段AB上,线段AC=12,BC=4,点M、N分别是AC、BC的中点,求MN的长度.