题目内容
18.已知多项式:A=2a2+ab-2a-1,B=a2+ab-1.(1)当a=-$\frac{1}{2}$,b=4时,求A-2B的值;
(2)若多项式C满足:C=A-2B-C,试用a、b的代数式表示C.
分析 (1)把A与B代入A-2B中,去括号合并得到最简结果,把a与b的值代入计算即可求出值;
(2)由C=A-2B-C,表示出C,将A与B代入,去括号合并即可得到结果.
解答 解:(1)∵A=2a2+ab-2a-1,B=a2+ab-1,
∴A-2B=2a2+ab-2a-1-2a2-2ab+2=-ab-2a+1,
当a=-$\frac{1}{2}$,b=4时,原式=2+1+1=4;
(2)由C=A-2B-C,得到C=$\frac{1}{2}$A-B=a2+$\frac{1}{2}$ab-a-$\frac{1}{2}$-a2-ab+1=-$\frac{1}{2}$ab-a+1.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.下列图形是中心对称图形的是( )
| A. | 平行四边形 | B. | 直角三角形 | C. | 等边三角形 | D. | 正五边形 |
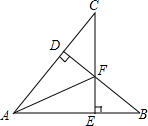 已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线.
已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线. (1)已知:如图,点C在线段AB上,线段AC=12,BC=4,点M、N分别是AC、BC的中点,求MN的长度.
(1)已知:如图,点C在线段AB上,线段AC=12,BC=4,点M、N分别是AC、BC的中点,求MN的长度.