题目内容
19.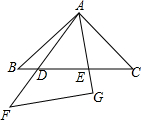 将两块完全相同的等腰直角三角板摆成如图所示的样式,给出下列结论:①AD•AE=DE•AB;②DF=EC;③∠BEA=∠DAC;④△BAE∽△CDA,其中正确的有①③④(填序号)
将两块完全相同的等腰直角三角板摆成如图所示的样式,给出下列结论:①AD•AE=DE•AB;②DF=EC;③∠BEA=∠DAC;④△BAE∽△CDA,其中正确的有①③④(填序号)
分析 ①证明△BAE∽△ADE即可得出,
②画图发现,DF和EC的长不确定,不一定相等;
③因为∠FAG=∠C=45°,所以根据外角定理得:∠BEA=45°+∠GAC,由角的和的关系得:∠DAC=45°+∠GAC,所以∠BEA=∠DAC;
④根据③中的结论加上一公共角,可得相似;
解答  解:①∵△ABC与△GAF是两块完全相同的等腰直角三角板,
解:①∵△ABC与△GAF是两块完全相同的等腰直角三角板,
∴∠B=∠DAE=45°,
∵∠BEA=∠AED,
∴△BAE∽△ADE,
∴AD:AB=DE:AE,
∴AD•AE=DE•AB;
故①正确;
②如图所示,EC不确定,根据旋转角度的不同,EC可能变长或变短,
∴DF不一定等于EC;
故②错误;
③∵∠BEA=∠C+∠GAC,
∵∠C=45°,
∴∠BEA=45°+∠GAC,
∵∠DAC=∠FAG+∠GAC,
∵∠FAG=45°,
∴∠DAC=45°+∠GAC,
∴∠BEA=∠DAC,
故③正确;
④∵∠BEA=∠DAC,∠B=∠C=45°
∴△BAE∽△CDA
故④正确;
所以正确的有:①③④;
故答案为:①③④.
点评 本题考查了三角形相似的性质和判定、等腰直角三角形的性质,等腰直角三角形的每个锐角为45°,在判定两个三角形相似时,应注意利用图形中已有的公共角这一隐含条件,对于乘积式的判定,要先化成比例式,再确定两个三角形,证明其相似.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
9. 有理数a,b在数轴上的位置如图所示,则下列结论中,正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论中,正确的是( )
 有理数a,b在数轴上的位置如图所示,则下列结论中,正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论中,正确的是( )| A. | a-b>0 | B. | a+b>0 | C. | $\frac{a}{b}$>0 | D. | |a|>|b| |
10.抛物线y=x2+2x-2的图象的顶点坐标是( )
| A. | (2,-2) | B. | (1,-2) | C. | (1,-3) | D. | (-1,-3) |
11.若|x-2|+(x-y-1)2=0,则多项式-y-(x2+2y2)的值为( )
| A. | -7 | B. | 5 | C. | -5 | D. | -13 |
8.一元二次方程x2+2x-2=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2)与B点.若C是y轴上的点,且满足△ABC的面积为10,则C点坐标为(0,1)或(0,-9).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2)与B点.若C是y轴上的点,且满足△ABC的面积为10,则C点坐标为(0,1)或(0,-9). 有理数a、b在数轴上的位置如图所示,在下列结论中:
有理数a、b在数轴上的位置如图所示,在下列结论中: