题目内容
10.抛物线y=x2+2x-2的图象的顶点坐标是( )| A. | (2,-2) | B. | (1,-2) | C. | (1,-3) | D. | (-1,-3) |
分析 把抛物线解析式化为顶点式可求得答案.
解答 解:
∵y=x2+2x-2=(x+1)2-3,
∴抛物线顶点坐标为(-1,-3),
故选D.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,顶点坐标为(h,k),对称轴为x=h.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知x、y为正数且$\sqrt{4-{x}^{2}}$+(3-y2)2=0,如果以x,y的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为( )
| A. | 5 | B. | 25 | C. | 7 | D. | 15 |
18.在-π,$\frac{1}{3}$,$\root{3}{4}$,0,$\sqrt{25}$,3.14,76.0123456…(小数部分由相继的正整数组成)中,无理数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
5.下面的说法中正确的为( )
| A. | -1不是单项式 | B. | -a表示负数 | ||
| C. | 1是绝对值最小的数 | D. | $x+\frac{1}{x}-1$不是多项式 |
15.化简|$\sqrt{2}$-1|+1的结果是( )
| A. | 2-$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
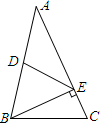 如图,在△ABC中,AB=AC,点D是AB的中点,BE⊥AC于点E.若DE=5cm,S△BEA=4S△BEC,则AE的长度是( )
如图,在△ABC中,AB=AC,点D是AB的中点,BE⊥AC于点E.若DE=5cm,S△BEA=4S△BEC,则AE的长度是( )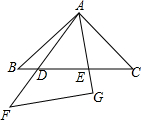 将两块完全相同的等腰直角三角板摆成如图所示的样式,给出下列结论:①AD•AE=DE•AB;②DF=EC;③∠BEA=∠DAC;④△BAE∽△CDA,其中正确的有①③④(填序号)
将两块完全相同的等腰直角三角板摆成如图所示的样式,给出下列结论:①AD•AE=DE•AB;②DF=EC;③∠BEA=∠DAC;④△BAE∽△CDA,其中正确的有①③④(填序号)