题目内容
1.解不等式组$\left\{\begin{array}{l}{2x+1≥0}\\{\frac{x+5}{3}-\frac{x}{2}>1}\end{array}\right.$,并把解集在是数轴上表示出来.分析 分别求出各不等式的解集,并在数轴上表示出来即可.
解答 解:$\left\{\begin{array}{l}{2x+1≥0①}\\{\frac{x+5}{3}-\frac{x}{2}>1②}\end{array}\right.$,由①得,x≥-$\frac{1}{2}$,
由②得,x<4,
故不等式组的解集为:-$\frac{1}{2}$≤x<4.
在数轴上表示为: .
.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.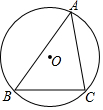 如图,点 O是△ABC外接圆的圆心,若⊙O的半径为5,∠A=45°,则$\widehat{BC}$的长是( )
如图,点 O是△ABC外接圆的圆心,若⊙O的半径为5,∠A=45°,则$\widehat{BC}$的长是( )
 如图,点 O是△ABC外接圆的圆心,若⊙O的半径为5,∠A=45°,则$\widehat{BC}$的长是( )
如图,点 O是△ABC外接圆的圆心,若⊙O的半径为5,∠A=45°,则$\widehat{BC}$的长是( )| A. | $\frac{5}{8}$π | B. | $\frac{25}{4}$π | C. | $\frac{5}{4}$π | D. | $\frac{5}{2}$π |
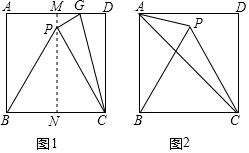 取一张正方形的纸片进行折叠,具体操作过程如下:
取一张正方形的纸片进行折叠,具体操作过程如下: 如图,点P为∠AOB平分线上的一点,PC⊥OB于点C,且PC=4,点P到OA的距离为4.
如图,点P为∠AOB平分线上的一点,PC⊥OB于点C,且PC=4,点P到OA的距离为4.
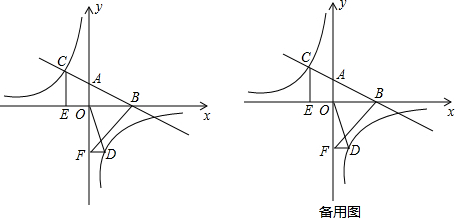
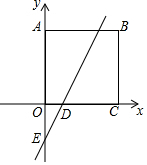 如图,矩形ABCD的顶点B坐标为(5,4),直线y=2x-3分别交x轴、y轴于D、E点,若线段BC上有一点P,直线DE上有一点Q,△APQ是以AP为斜边的等腰直角三角形,则点P坐标为(5,1)或(5,3).
如图,矩形ABCD的顶点B坐标为(5,4),直线y=2x-3分别交x轴、y轴于D、E点,若线段BC上有一点P,直线DE上有一点Q,△APQ是以AP为斜边的等腰直角三角形,则点P坐标为(5,1)或(5,3).