题目内容
11.在“母亲节”期间,某校部分团员参加社会公益活动,准备构建一批许愿瓶进行销售,并将所得利润捐给慈善机构,根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如表所示:(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;为了方便顾客,售价定位多少时可获利1200元;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定此时的销售单价,并求出此时的最大利润.
| z(元/个) | 16 | 14 | 12 | 10 |
| y(个) | 120 | 180 | 240 | 300 |
分析 (1)观察图表可得该函数图象是一次函数,设出一次函数解析式,把其中两点代入即可求得该函数解析式,进而把其余两点的横坐标代入看纵坐标是否与点的纵坐标相同;
(2)根据销售利润=每个许愿瓶的利润×销售量列出函数表达式;令W=1200,解方程即可.
(3)根据进货成本可得自变量的取值,结合二次函数的关系式即可求得相应的最大利润.
解答 解:(1)y是x的一次函数,设y=kx+b图象过点(10,300),(12,240),
$\left\{\begin{array}{l}{10k+b=300}\\{12k+b=240}\end{array}\right.$,
解得
$\left\{\begin{array}{l}{k=-30}\\{b=600}\end{array}\right.$,
故y与x 之间的函数关系为:y=-30x+600,
当x=14时,y=180;当x=16时,y=120,
即点(14,180),(16,120)均在函数y=-30x+600的图象上.
∴y与x之间的函数关系式为y=-30x+600;
(2)w=(x-6)(-30x+600)=-30x2+780x-3600
即w与x之间的函数关系式为w=-30x2+780x-3600;
令W=1200,则-30x2+780x-3600=1200,
解得:x1=10,x2=16,
因为了方便顾客,所以售价定位为10元时可获利1200元.
(3)由题意得6(-30x+600)≤900,解得x≥15.
w=-30x2+780x-3600=-30(x-13)2+1350,
∵对称轴为x=13,a=-30<0,
∴抛物线开口向下,当x≥15时,w随x增大而减小,
∴当x=15时,w最大=1350.
即以15元/个的价格销售这批许愿瓶可获得最大利润1350元.
点评 此题主要考查了二次函数的最值问题、利用待定系数法求一次函数得解析式、掌握待定系数法求一次函数的解析式以及配方法求二次函数的最值是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 12-9-6 | B. | 12+9-6 | C. | -12+9+6 | D. | 12-9+6 |
 已知,如图?ABCD中,E为AD边上的一点,AE:ED=2:5,连结AC、BE交于点F,若AC=20cm,则AF=$\frac{40}{9}$,CF=$\frac{140}{9}$.
已知,如图?ABCD中,E为AD边上的一点,AE:ED=2:5,连结AC、BE交于点F,若AC=20cm,则AF=$\frac{40}{9}$,CF=$\frac{140}{9}$.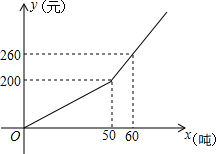 已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.