题目内容
12.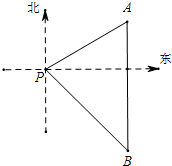 一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的东南方向上的B处.这时,海轮所在的B处距离灯塔P有多远?(结果保留根号)
一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的东南方向上的B处.这时,海轮所在的B处距离灯塔P有多远?(结果保留根号)
分析 在Rt△APC中,求出PC的长,再在Rt△PBC中,求出CB的长,将AC和CB相加即可.
解答  解:∵∠APC=90°-60°=30°,AP=80海里,
解:∵∠APC=90°-60°=30°,AP=80海里,
∴PC=AP•cos30°=80×$\frac{\sqrt{3}}{2}$=40$\sqrt{3}$海里,AC=AP•sin30°=80×$\frac{1}{2}$=40(海里),
又∵∠BPC=45°,
∴CB=PC=40$\sqrt{3}$海里,
∴BP=$\sqrt{2}$×40$\sqrt{3}$=40$\sqrt{6}$(海里).
点评 本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
7.下列从左到右的变形,是分解因式的是( )
| A. | (a+3)(a-3)=a2-9 | B. | x2+x-5=(x-2)(x+3)+1 | C. | a2b+ab2=ab(a+b) | D. | x2+1=x(x+$\frac{1}{x}$) |
2.下列各组中的两个量,不是具有相反意义的是( )
| A. | 买进20棵树苗与种树10棵 | |
| B. | 一辆出租车向北行驶24米与向南行驶15米 | |
| C. | 盈利50元与亏损40元 | |
| D. | 气温升高3℃与气温降低5℃ |
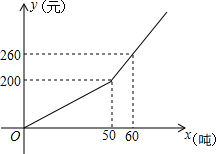 已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.