题目内容
16.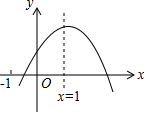 已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a-b+c<0;③2a+b-c<0;④4a+2b+c>0,⑤若点(-$\frac{2}{3}$,y1)和($\frac{7}{3}$,y2)在该图象上,则y1>y2.其中正确的结论是②③④(填入正确结论的序号)
已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a-b+c<0;③2a+b-c<0;④4a+2b+c>0,⑤若点(-$\frac{2}{3}$,y1)和($\frac{7}{3}$,y2)在该图象上,则y1>y2.其中正确的结论是②③④(填入正确结论的序号)
分析 由二次函数的开口方向,对称轴x=1,以及二次函数与y的交点在x轴的上方,与x轴的交点的位置等条件来判断各结论的正误即可.
解答 解:∵抛物线开口向下,
∴a<0,
∵对称轴在y轴右边,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
∵二次函数y=ax2+bx+c图象可知,当x=-1时,y<0,
∴a-b+c<0,故②正确;
∵二次函数图象的对称轴是直线x=1,c>0,
∴-$\frac{b}{2a}$=1,
∴2a+b=0,
∴2a+b<c,
∴2a+b-c<0,故③正确;
∵二次函数y=ax2+bx+c图象可知,当x=2时,y>0,
∴4a+2b+c>0,故④正确;
∵二次函数图象的对称轴是直线x=1,
∴抛物线上x=-$\frac{2}{3}$时的点与当x=$\frac{8}{3}$时的点对称,
∵x>1,y随x的增大而减小,
∴y1<y2,故⑤错误;
故答案为:②③④.
点评 本题考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
11.有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
| 甲种糖果 | 乙种糖果 | 丙种糖果 | |
| 单价(元/千克) | 20 | 25 | 30 |
| 千克数 | 40 | 40 | 20 |
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
1.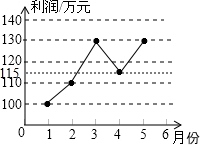 某企业1-5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( )
某企业1-5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( )
 某企业1-5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( )
某企业1-5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( )| A. | 1-5月份利润的众数是130万元 | |
| B. | 1-4月份利润的极差与1-5月份利润的极差不同 | |
| C. | 1-2月份利润的增长快于2-3月份利润的增长 | |
| D. | 1-5月份利润的中位数是130万元 |
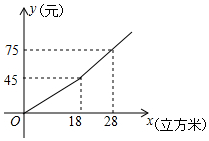 某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
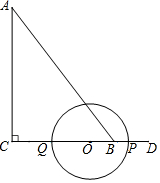 如图,在△ABC中,∠ACB=90°,AC=8,CB=6,点D在线段CB的延长线上,且BD=2,点P从点D出发沿着DC向终点C以每秒1个单位的速度运动,同时点Q从点C出发沿着折线C-B-A往终点A以每秒2个单位的速度运动.以PQ为直径构造⊙O,设运动的时间为t(t≥0)秒.
如图,在△ABC中,∠ACB=90°,AC=8,CB=6,点D在线段CB的延长线上,且BD=2,点P从点D出发沿着DC向终点C以每秒1个单位的速度运动,同时点Q从点C出发沿着折线C-B-A往终点A以每秒2个单位的速度运动.以PQ为直径构造⊙O,设运动的时间为t(t≥0)秒.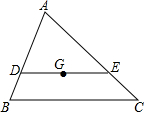 如图,G为△ABC的重心,DE过点G,且DE∥BC,交AB、AC,分别于D、E两点,则△ADE与△ABC的面积之比为$\frac{4}{9}$.
如图,G为△ABC的重心,DE过点G,且DE∥BC,交AB、AC,分别于D、E两点,则△ADE与△ABC的面积之比为$\frac{4}{9}$.