题目内容
13.设x1,x2是方程2x2+4x-3=0的两个根,利用根与系数的关系,求下列各式的值:(1)(x1+1)(x2+1);
(2)x12+x22;
(3)$\frac{x_2}{x_1}+\frac{x_1}{x_2}$;
(4)(x1-x2)2.
分析 根据一元二次方程根与系数的关系,可以求得方程两根的和与两根的积,可把要求的各式子都整理成两根的和与两根的积的形式,把两根的和与两根的积的值代入即可求解.
解答 解:∵x1,x2是方程2x2+4x-3=0的两个根,
∴x1+x2=-2,x1x2=-1.5.
(1)原式=x1x2+(x1+x2)+1=-2.5.
(2)原式=(x1+x2)2-2x1x2=7.
(3)原式=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{14}{3}$.
(4)原式=(x1+x2)2-4x1x2=10.
点评 本题考查的是根与系数的关系,即若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目

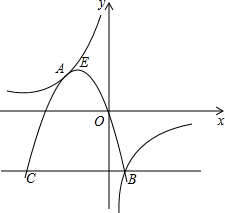 如图,抛物线y=ax2+bx+c(a<0)与双曲线相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.
如图,抛物线y=ax2+bx+c(a<0)与双曲线相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.