题目内容
9.正比例函数与一次函数的图象交于点(-1,2),两图象与x轴围成的三角形的面积为6.求一次函数的解析式.分析 设正比例函数解析式为y=kx,则把点(-1,2)代入可求出k的值,从而得到正比例函数解析式;设一次函数解析式为y=mx+n,则一次函数与y轴的交点B的坐标为(0,n),利用三角形面积公式得到$\frac{1}{2}$|n|•2=6,解得n=6或n=-6,然后分类讨论:把A(-1,2)分别代入y=mx+6和y=mx-6中,计算出对应的m的值,于是可得到一次函数解析式.
解答 解:如图,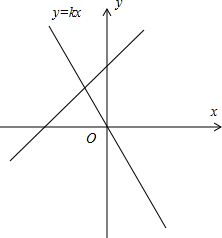
设正比例函数解析式为y=kx,
把点(-1,2)代入得-k=2,解得k=-2,
所以正比例函数解析式为y=-2x;
设一次函数解析式为y=mx+n,则一次函数与y轴的交点的坐标为(0,n),
因为$\frac{1}{2}$|n|•3=6,
所以n=6或n=-6,
把点(-1,2)代入y=mx+6得-m+6=2,解得m=4,此时一次函数解析式为y=4x+6;
把点(-1,2)代入y=mx-6得-m-6=2,解得m=-8,此时一次函数解析式为y=-8x-6;
所以正比例函数解析式为y=-2x,一次函数解析式为y=4x+6或y=-8x-6.
点评 此题考查待定系数法求函数解析式,三角形的面积,利用三角形的面积分类得出一次函数与y轴的交点坐标是解决问题的关键.

练习册系列答案
相关题目
20.若关于x的分式方程$\frac{2x-m}{n-2x}$=$\frac{p}{q}$有解,则必须满足条件( )
| A. | m≠n | B. | m≠-n | C. | np≠-mq | D. | p≠-q,m≠n |
 如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.
如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.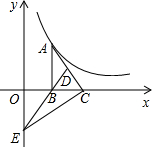 如图,Rt△ABC的直角边BC在x轴正半轴上,点D为AC上一点,且AD=3DC,BD的反向延长线交y轴负半轴于E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BEC=6,则k=36.
如图,Rt△ABC的直角边BC在x轴正半轴上,点D为AC上一点,且AD=3DC,BD的反向延长线交y轴负半轴于E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BEC=6,则k=36.