题目内容
15.计算:(-45)÷[(-$\frac{1}{3}$)÷(-$\frac{2}{5}$)].分析 首先根据有理数的除法法则,求出(-$\frac{1}{3}$)÷(-$\frac{2}{5}$)的值是多少;然后用-45除以所得的商,求出算式(-45)÷[(-$\frac{1}{3}$)÷(-$\frac{2}{5}$)]的值是多少即可.
解答 解:(-45)÷[(-$\frac{1}{3}$)÷(-$\frac{2}{5}$)]
=(-45)÷$\frac{5}{6}$
=-54.
点评 此题主要考查了有理数的除法,要熟练掌握,解答此题的关键是要熟练掌握有理数的除法法则.

练习册系列答案
相关题目
5.下列各式从左至右的变形中,一定正确的是( )
| A. | $\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$ | B. | $\sqrt{{a}^{2}}$=a | C. | $\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$ | D. | $\sqrt{\frac{x}{y}}$=$\frac{\sqrt{x}}{\sqrt{y}}$ |
6.x与$\frac{2}{3}$的差的一半是正数,用不等式表示为( )
| A. | $\frac{1}{2}$(x-$\frac{2}{3}$)>0 | B. | $\frac{1}{2}$x-$\frac{2}{3}$<0 | C. | $\frac{1}{2}$x-$\frac{2}{3}$>0 | D. | $\frac{1}{2}$(x-$\frac{2}{3}$)<0 |
10.⊙O过点B,C,圆心O在等腰直角△ABC内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 3$\sqrt{2}$ |
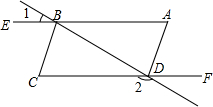 如图,AE∥CF,∠A=∠C.
如图,AE∥CF,∠A=∠C.

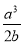 、
、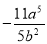 、
、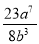 、
、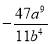 、……(
、……(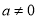 ,
, 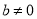 ),则第五个分式是__________________ ,第
),则第五个分式是__________________ ,第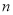 个分式是__________________ ;
个分式是__________________ ;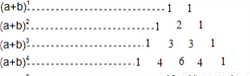
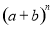 展开式中共有多少项?
展开式中共有多少项?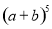 的展开式?
的展开式?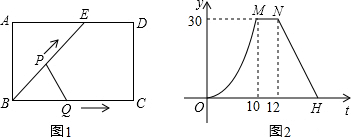 如图1,点E为矩形ABCD的边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系如图2(曲线OM为抛物线的一部分),则下列结论:
如图1,点E为矩形ABCD的边AD上一点,点P、点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系如图2(曲线OM为抛物线的一部分),则下列结论: