题目内容
7.解不等式:(1)$\frac{0.1x-1}{0.5}$-$\frac{5-x}{2}$≤$\frac{0.03-0.01x}{0.02}$;
(2)$\frac{x}{1×2}$+$\frac{x}{2×3}$+$\frac{x}{3×4}$+…+$\frac{x}{2013×2014}$>-2013.
分析 (1)首先把原不等式变形,再去分母,去括号,移项,合并同类项,系数化为1即可;
(2)根据$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,…,把原不等式变形,即可得出结果.
解答 解:(1)原不等式可化为:$\frac{x-10}{5}-\frac{5-x}{2}≤\frac{3-x}{2}$,
去分母得:2(x-10)-5(5-x)≤5(3-x),
去括号,移项,合并同类项得:12x≤60,
系数化为1得:x≤5;
(2)原不等式可化为:x(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2013}$-$\frac{1}{2014}$)x>-2013,
整理得:$\frac{2013}{2014}$x>-2013,
系数化为1得:x>-2014.
点评 本题考查了一元一次不等式的解法、分数的基本性质等知识;熟练掌握一元一次不等式的解法,把(2)正确变形是解决问题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图,△OAB是等边三角形,过点A的直线l:y=-$\frac{\sqrt{3}}{3}$x+m与x轴交于点E(4,0)
如图,△OAB是等边三角形,过点A的直线l:y=-$\frac{\sqrt{3}}{3}$x+m与x轴交于点E(4,0) 如图,在圆心角为90°的扇形OAB中,半径OA=4,C为$\widehat{AB}$的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为2π+2$\sqrt{2}$-2.
如图,在圆心角为90°的扇形OAB中,半径OA=4,C为$\widehat{AB}$的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为2π+2$\sqrt{2}$-2.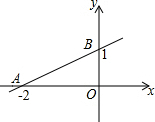 一次函数y=ax+b的图象经过点A、点B,如图所示,则不等式0<ax+b<1的解集是-2<x<0.
一次函数y=ax+b的图象经过点A、点B,如图所示,则不等式0<ax+b<1的解集是-2<x<0.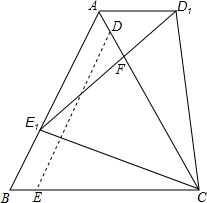 如图,在等边△ABC与等边△CDE中D、E分别在边AC、BC上,且DE∥AB,BC=4$\sqrt{3}$,CE=$\sqrt{39}$,将△CED绕着C点顺时针旋转到△CD1E1,记线段AC与线段E1D1的交点为F,当E点落在AB边上的时候停止旋转,问此时CF的长为$\frac{13}{4}$$\sqrt{3}$.
如图,在等边△ABC与等边△CDE中D、E分别在边AC、BC上,且DE∥AB,BC=4$\sqrt{3}$,CE=$\sqrt{39}$,将△CED绕着C点顺时针旋转到△CD1E1,记线段AC与线段E1D1的交点为F,当E点落在AB边上的时候停止旋转,问此时CF的长为$\frac{13}{4}$$\sqrt{3}$.