题目内容
18. 如图,在圆心角为90°的扇形OAB中,半径OA=4,C为$\widehat{AB}$的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为2π+2$\sqrt{2}$-2.
如图,在圆心角为90°的扇形OAB中,半径OA=4,C为$\widehat{AB}$的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为2π+2$\sqrt{2}$-2.
分析 连接OC、EC,由△OCD≌△OCE、OC⊥DE可得DE=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,分别求出S扇形OBC、S△OCD、S△ODE面积,根据S扇形OBC+S△OCD-S△ODE=S阴影部分可得.
解答 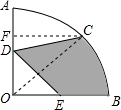 解:连结OC,过C点作CF⊥OA于F,
解:连结OC,过C点作CF⊥OA于F,
∵半径OA=4,C为$\widehat{AB}$的中点,D、E分别是OA、OB的中点,
∴OD=OE=2,OC=4,∠AOC=45°,
∴CF=2$\sqrt{2}$,
∴空白图形ACD的面积=扇形OAC的面积-三角形OCD的面积
=$\frac{45π×{4}^{2}}{360}$-$\frac{1}{2}$×2×2$\sqrt{2}$
=2π-2$\sqrt{2}$,
三角形ODE的面积=$\frac{1}{2}$OD×OE=2,
∴图中阴影部分的面积=扇形OAB的面积-空白图形ACD的面积-三角形ODE的面积
=$\frac{90π×{4}^{2}}{360}$-(2π-2$\sqrt{2}$)-2
=2π+2$\sqrt{2}$-2.
故答案为:2π+2$\sqrt{2}$-2.
点评 考查了扇形面积的计算,本题难点是得到空白图形ACD的面积,关键是理解图中阴影部分的面积=扇形OAB的面积-空白图形ACD的面积-三角形ODE的面积.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
13.下列各数中,大小在-1和-2之间的数是( )
| A. | -3 | B. | -$\sqrt{2}$ | C. | 0 | D. | |-3| |
3.某超市计划购进甲、乙两种品牌的新型节能台灯20盏,这两种台灯的进价和售价如下表所示:
设购进甲种台灯x盏,且所购进的两种台灯都能全部卖出.
(1)若该超市购进这批台灯共用去1000元,问这两种台灯购进多少盏?
(2)若购进两种台灯的总费用不超过1100元,那么超市如何进货才能获得最大利润?最大利润是多少?
(3)最终超市按照(2)中的方案进货,但实际销售中,由于乙品牌的台灯销售前景不容乐观,超市计划对乙品牌台灯进行降价销售,当毎盏台灯最多降价10元时,全部销售后才能使利润不低于550元.
| 甲 | 乙 | |
| 进价(元/件) | 40 | 60 |
| 售价(元/件) | 60 | 100 |
(1)若该超市购进这批台灯共用去1000元,问这两种台灯购进多少盏?
(2)若购进两种台灯的总费用不超过1100元,那么超市如何进货才能获得最大利润?最大利润是多少?
(3)最终超市按照(2)中的方案进货,但实际销售中,由于乙品牌的台灯销售前景不容乐观,超市计划对乙品牌台灯进行降价销售,当毎盏台灯最多降价10元时,全部销售后才能使利润不低于550元.
 如图是一个正方体的展开图,折叠成正方体后与“中”字相对的一面上的字是顺.
如图是一个正方体的展开图,折叠成正方体后与“中”字相对的一面上的字是顺.


