题目内容
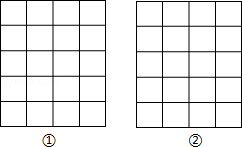
17.如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图:(1)在图①中画一条线段MN,使MN=$\sqrt{5}$;
(2)在图②中画一个△ABC,使其三边长分别为3,$\sqrt{10}$,$\sqrt{13}$.
分析 (1)如图①,在直角三角形MQN中,利用勾股定理求出MN的长为$\sqrt{5}$,故MN为所求线段;
(2)如图②,分别利用勾股定理求出AB,AC,以及BC的长,即可确定出所求△ABC.
解答  解:(1)如图①所示,在Rt△MQN中,MQ=2,NQ=1,
解:(1)如图①所示,在Rt△MQN中,MQ=2,NQ=1,
根据勾股定理得:MN=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
则线段MN为所求的线段;
(2)如图②所示,AB=3,AC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,BC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
则△ABC为所求三角形.
点评 此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
8.找出以下图形变化的规律,则第2015个图形中黑色正方形的数量是( )


| A. | 3020 | B. | 3021 | C. | 3022 | D. | 3023 |

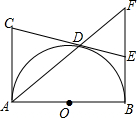 如图,AB是半圆O的直径,AC⊥AB,CD切半圆于点D,BF⊥AB,交AD的延长线于F,交CD的延长线于E.
如图,AB是半圆O的直径,AC⊥AB,CD切半圆于点D,BF⊥AB,交AD的延长线于F,交CD的延长线于E.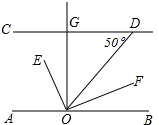 如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠D=50°,则下列结论:
如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠D=50°,则下列结论: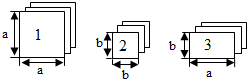 如图,有足够多的长方形和正方形卡片,
如图,有足够多的长方形和正方形卡片,