题目内容
12.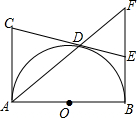 如图,AB是半圆O的直径,AC⊥AB,CD切半圆于点D,BF⊥AB,交AD的延长线于F,交CD的延长线于E.
如图,AB是半圆O的直径,AC⊥AB,CD切半圆于点D,BF⊥AB,交AD的延长线于F,交CD的延长线于E.(1)若∠C=80°,求∠F的度数;
(2)求证:BE=EF;
(3)若AC=6,BE=4,求AB的长.
分析 (1)先证明AC、BF是半圆O的切线,AC∥BF,得出∠F=∠CAD,再由切线长定理得出CA=CD,BE=DE,求出∠CAD=∠CDA,即可求出∠F;
(2)连接BD,求出∠F=∠EDF,DE=EF,再由(1)中BE=DE,即可得出结论;
(3)作EG⊥AC于G,则四边形ABEG是矩形,得出AG=BE=4,EG=AB,求出CE、CG,根据勾股定理求出EG,即可得出AB.
解答 (1)解:∵AB是半圆O的直径,AC⊥AB,BF⊥AB,
∴AC、BF是半圆O的切线,AC∥BF,
∴∠F=∠CAD,
∵CD切半圆于点D,
∴CA=CD,BE=DE,
∴∠CAD=∠CDA=50°,
∴∠F=50°;
(2)证明:连接BD,如图所示: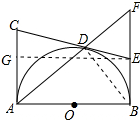
则∠ADB=90°,
∴∠BDF=90°,
∵∠EDF=∠CDA=50°,
∴∠F=∠EDF,
∴DE=EF,
∴BE=EF;
(3)解:作EG⊥AC于G,如图所示:
则四边形ABEG是矩形,
∴AG=BE=4,EG=AB,
∵AC=CD=6,DE=BE=4,
∴CE=6+4=10,CG=6-4=2,
∴EG=$\sqrt{1{0}^{2}-{2}^{2}}$=4$\sqrt{6}$,
∴AB=4$\sqrt{6}$.
点评 本题考查了切线的判定与性质、切线长定理、等腰三角形的判定、勾股定理的运用;熟练掌握切线的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
7.下列计算正确的是( )
| A. | a8÷a4=a2 | B. | x2+x3=x5 | C. | (-c3)•(-c)5=c8 | D. | (-x-y)(-x+y)=-x2+y2 |
1.在平面直角坐标系中,将点A(-2,1)向左平移2个单位,再向上平移3个单位到点Q,则点Q的坐标为( )
| A. | (-2,3) | B. | (0,-2) | C. | (-4,4) | D. | (-4,-2) |