题目内容
2.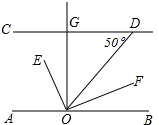 如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠D=50°,则下列结论:
如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠D=50°,则下列结论:①∠AOE=65°;②OF平分∠BOD;③∠GOE=∠DOF;④∠GOE=25°.
其中正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
分析 由平行线的性质结合角平分线的定义,再结合垂直的定义,可分别求得∠AOE、∠GOE、∠DOF、∠BOD,可判定结论,得出正确答案.
解答 解:∵AB∥CD,
∴∠BOD=∠CDO=50°,
∴∠AOD=180°-50°=130°,
又∵OE平分∠AOD,
∴∠AOE=$\frac{1}{2}$∠AOD=65°,
故①正确;
∵OG⊥CD,
∴∠GOA=∠DGO=90°,
∴∠GOD=40°,∠GOE=90°-∠AOE=25°,
∴∠EOG+∠GOD=65°,
又OE⊥OF,
∴∠DOF=25°,
∴∠BOF=∠DOF=25°,
∴OF平分∠BOD,∠GOE=∠DOF,故②③④正确;
故选D.
点评 本题考查了平行线的性质,以及垂线的定义,用到的知识点为:两直线平行,内错角相等,两直线平行,同旁内角互补;垂直于平行线中的一条,必垂直于另一条.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
13.在2,-$\sqrt{3}$,0,π这四个数中,最小的一个数是( )
| A. | -$\sqrt{3}$ | B. | 0 | C. | 2 | D. | π |
11. 如图.已知直线a,b被直线c所截,且a∥b,∠1=42°,那么∠2的度数为( )
如图.已知直线a,b被直线c所截,且a∥b,∠1=42°,那么∠2的度数为( )
 如图.已知直线a,b被直线c所截,且a∥b,∠1=42°,那么∠2的度数为( )
如图.已知直线a,b被直线c所截,且a∥b,∠1=42°,那么∠2的度数为( )| A. | 42° | B. | 48° | C. | 52° | D. | 132° |
 如图,同学们上体育课时,老师测量学生的跳远成绩,其测量的主要依据是垂线段最短.
如图,同学们上体育课时,老师测量学生的跳远成绩,其测量的主要依据是垂线段最短.