题目内容
已知：如图，⊙O的直径AD=2， |
| BC |
|
| CD |
|
| DE |
（1）求证：AB=BC；
（2）求五边形ABCDE的面积．
考点：圆周角定理,圆心角、弧、弦的关系
专题：
分析：（1）连接BE，根据∠BAE=90°可知BE是⊙O的直径，故可得出
+
+
=90°，再根据
+
+
=90°可得出
=
，再由
=
=
可得出
=
，由此可得出结论．
（2）过B作BF⊥AC，垂足为F，先根据ASA定理得出△ACD≌△AED，再求出S△ACD=S△AED=
AC•CD=
，由S五边形ABCDE=S△ABC+2S△ACD=即可得出结论．
|
| BC |
|
| CD |
|
| DE |
|
| AB |
|
| BC |
|
| CD |
|
| AB |
|
| DE |
|
| BC |
|
| CD |
|
| DE |
|
| AB |
|
| BC |
（2）过B作BF⊥AC，垂足为F，先根据ASA定理得出△ACD≌△AED，再求出S△ACD=S△AED=
| 1 |
| 2 |
| ||
| 2 |
解答：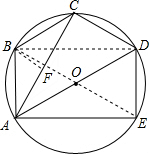
（1）证明：连接BE，
∵∠BAE=90°，
∴BE是⊙O的直径，
∴
+
+
=90°．
∵
+
+
=90°，
∴
=
．
∵
=
=
，
∴
=
，
∴AB=BC；
（2）解：连接BD，
∵
=
，
∴∠CAD=∠EAD，
∵AD是⊙O的直径，
∴∠ACD=∠AED=90°．
在△ACD与△AED中，
，
∴△ACD≌△AED（SAS）．
∵在Rt△ACD中，AD=2，∠CAD=30°，
∴CD=2sin30°=1，AC=2cos30°=
，
∴S△ACD=S△AED=
AC•CD=
∵AD为直径，
∴∠ABD=90°
又∵∠BAD=∠BAC+∠CAD=60°，
∴∠BDA=30°
∴∠BCA=∠BDA=30°，
∴∠BAC=∠BCA，
∴BA=BC
过B作BF⊥AC，垂足为F，
∴AF=
AC=
，
∴BF=AFtan30°=
，
∴S△ABC=
AC•BF=
，
∴S五边形ABCDE=S△ABC+2S△ACD=
+2×
×
=
．
（1）证明：连接BE，∵∠BAE=90°，
∴BE是⊙O的直径，
∴
|
| BC |
|
| CD |
|
| DE |
∵
|
| AB |
|
| BC |
|
| CD |
∴
|
| AB |
|
| DE |
∵
|
| BC |
|
| CD |
|
| DE |
∴
|
| AB |
|
| BC |
∴AB=BC；
（2）解：连接BD，
∵
|
| CD |
|
| DE |
∴∠CAD=∠EAD，
∵AD是⊙O的直径，
∴∠ACD=∠AED=90°．
在△ACD与△AED中，
|
∴△ACD≌△AED（SAS）．
∵在Rt△ACD中，AD=2，∠CAD=30°，
∴CD=2sin30°=1，AC=2cos30°=
| 3 |
∴S△ACD=S△AED=
| 1 |
| 2 |
| ||
| 2 |
∵AD为直径，
∴∠ABD=90°
又∵∠BAD=∠BAC+∠CAD=60°，
∴∠BDA=30°
∴∠BCA=∠BDA=30°，
∴∠BAC=∠BCA，
∴BA=BC
过B作BF⊥AC，垂足为F，
∴AF=
| 1 |
| 2 |
| ||
| 2 |
∴BF=AFtan30°=
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 4 |
∴S五边形ABCDE=S△ABC+2S△ACD=
| ||
| 4 |
| 1 |
| 2 |
| 3 |
5
| ||
| 4 |
点评：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
黄冈创优卷系列答案
相关题目
如图，在矩形ABCD中，对角线AC、BD相交于G，E为AD的中点，连接BE交AC于F，连接FD，若∠BFA=90°，则下列四对三角形：①△BEA与△ACD；②△FED与△DEB；③△CFD与△ABG；④△ADF与△EFD，其中相似的为（ ）| A、①④ | B、①② |
| C、②③④ | D、①②③④ |
三个皮带轮的半径都是1，圆中心距离AC=3，BC=3
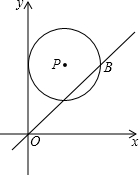如图，在平面直角坐标系中，⊙P的圆心是（4，a）（a＞4），半径为4，函数y=x的图象被⊙P截得的弦AB的长为4| 3 |
A、2
| ||
B、2
| ||
C、4+2
| ||
D、4+2
|
