题目内容
10.在直角坐标系中画出函数y=$\frac{1}{2}$(x-3)2的图象(1)指出该函数图象的开口方向、顶点坐标和对称轴;
(2)试说明函数与二次函数y=$\frac{1}{2}$x2的图象的关系;
(3)根据图象说明何时y有最大(小)值,是多少.
分析 (1)根据图象即可求得开口方向、顶点坐标和对称轴.
(2)根据二次函数y=$\frac{1}{2}$x2的图象的性质,结合函数y=$\frac{1}{2}$(x-3)2的图象即可求得;
(3)根据图象说明即可.
解答 解:函数y=$\frac{1}{2}$(x-3)2的图象如图所示: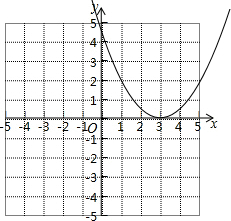
(1)函数图象的开口方向向上、顶点坐标(3,0)和对称轴为x=3;
(2)函数与二次函数y=$\frac{1}{2}$x2的图象的关系:二次函数y=$\frac{1}{2}$x2的图象箱左平移三个单位得到函数y=$\frac{1}{2}$(x-3)2的图象;
(3)y有最小值,最小值为0.
点评 本题考查了二次函数的性质,解题的关键是确定二次函数的顶点坐标及对称轴.

练习册系列答案
相关题目
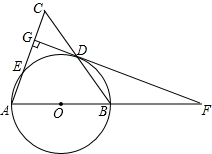 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.