题目内容
5.一列队伍长100米正在行进,传令兵从排尾走到排头,又从排头走到排尾,这列队伍正好前进了100米,已知队伍的速度和传令兵的速度保持不变,求传令兵走了多少米?分析 设传令兵的速度为V1,队伍的速度为V2,传令兵从队尾到队头的时间为t1,从队头到队尾的时间为t2,队伍前进用时间为t.以队伍为参照物,可求传令兵从队尾往队头的速度,从队头往队尾的速度,利用速度公式求通讯员从队尾到队头的时间t1,传令兵从队头到队尾的时间为t2,队伍前进100用的时间t,而t=t1+t2,据此列方程求出V1、V2的关系,进而求出在t时间内传令兵行走的路程.
解答 解:设传令兵的速度为V1,队伍的速度为V2,传令兵从队尾到队头的时间为t1,从队头到队尾的时间为t2,队伍前进用时间为t.
由传令兵往返总时间与队伍运动时间相等可得如下方程:
t=t1+t2,
即:$\frac{100}{{v}_{2}}$=$\frac{100}{{v}_{1}{-v}_{2}}$+$\frac{100}{{v}_{1}+{v}_{2}}$,
整理上式得:V12-2V1V2-V22=0
解得:v1=($\sqrt{2}$+1)v2;
将上式等号两边同乘总时间t,
即V1t=($\sqrt{2}$+1)v2t
V1t即为传令兵走过的路程S1,V2t即为队伍前进距离S2,则有
S1=($\sqrt{2}$+1)S2=($\sqrt{2}$+1)100m.
答:传令兵在这过程中所走的路程($\sqrt{2}$+1)100m.
点评 本题考查了应用类问题,关键是计算向前的距离和向后的距离,难点是知道向前的时候人和队伍前进方向相同,向后的时候人和队伍前进方向相反,解决此类问题常常用到相对运动的知识.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
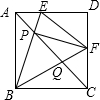 如图,E是正方形ABCD中AD边上的一个动点,AC与BE交于点P,过P点作PF⊥BE交CD边于F点,连结EF、BF,若AB=4,下列结论
如图,E是正方形ABCD中AD边上的一个动点,AC与BE交于点P,过P点作PF⊥BE交CD边于F点,连结EF、BF,若AB=4,下列结论