题目内容
11.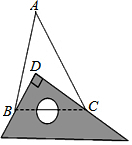 如图,已知在△ABC中,∠A=40°,将一块直角三角板放在△ABC上使三角板的两条直角边分别经过B、C,直角顶点D落在△ABC的内部,那么∠ABD+∠ACD=50度.
如图,已知在△ABC中,∠A=40°,将一块直角三角板放在△ABC上使三角板的两条直角边分别经过B、C,直角顶点D落在△ABC的内部,那么∠ABD+∠ACD=50度.
分析 根据三角形内角和定理可得∠ABC+∠ACB=180°-∠A=140°,∠DBC+∠DCB=180°-∠DBC=90°,进而可求出∠ABD+∠ACD的度数.
解答 解:在△ABC中,∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°,
在△DBC中,∵∠BDC=90°,
∴∠DBC+∠DCB=180°-90°=90°,
∴∠ABD+∠ACD=140°-90°=50°;
故答案是:50.
点评 本题考查三角形外角的性质及三角形的内角和定理,实际上证明了三角形的外角和是360°,解答的关键是沟通外角和内角的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列各式中,不是最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
4.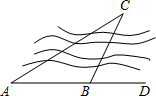 如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )
如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )
 如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )
如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )| A. | 100米 | B. | 100$\sqrt{3}$米 | C. | 200米 | D. | 200$\sqrt{3}$米 |
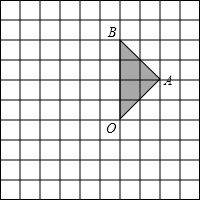 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ABO的三个顶点A、B、O都在格点上.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ABO的三个顶点A、B、O都在格点上. 如图,已知D是△ABC的边BC上一点,AB=AC=BD,AD=CD,求∠B的度数.
如图,已知D是△ABC的边BC上一点,AB=AC=BD,AD=CD,求∠B的度数.