题目内容
20.先化简,再求值:$(\frac{x}{2x+4}+\frac{1}{x-2})$÷$\frac{{x}^{2}+4}{x+2}$,其中x=1010.分析 首先把括号里面的通分,然后计算同分母的加法,再计算除法,先变成乘法,再约分后相乘,化简后,再代入x的值.
解答 解:原式=[$\frac{x(x-2)}{2(x+2)(x-2)}$+$\frac{2(x+2)}{2(x-2)(x+2)}$]•$\frac{x+2}{{x}^{2}+4}$,
=$\frac{{x}^{2}+4}{2(x+2)(x-2)}$$•\frac{x+2}{{x}^{2}+4}$,
=$\frac{1}{2(x-2)}$,
当x=1010时,原式=$\frac{1}{2×(1010-2)}$=$\frac{1}{2016}$.
点评 此题主要考查了分式的化简求值,关键是掌握在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.菱形的两条对角线长分别为9cm和4cm,则此菱形的面积是( )
| A. | 16cm2 | B. | 4$\sqrt{13}$cm2 | C. | 18cm2 | D. | 2$\sqrt{13}$cm2 |
5.下列计算正确的是( )
| A. | 23=6 | B. | -32=9 | C. | (-1)2=1 | D. | 2÷6×$\frac{1}{3}$=1 |
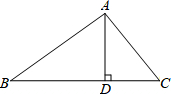 如图,在△ABC中,AD⊥BC,AB=5,BD=4,CD=$\sqrt{3}$.
如图,在△ABC中,AD⊥BC,AB=5,BD=4,CD=$\sqrt{3}$.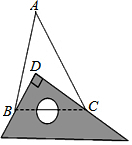 如图,已知在△ABC中,∠A=40°,将一块直角三角板放在△ABC上使三角板的两条直角边分别经过B、C,直角顶点D落在△ABC的内部,那么∠ABD+∠ACD=50度.
如图,已知在△ABC中,∠A=40°,将一块直角三角板放在△ABC上使三角板的两条直角边分别经过B、C,直角顶点D落在△ABC的内部,那么∠ABD+∠ACD=50度.