Question

5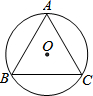．如图，⊙O是等边三角形ABC的外接圆，⊙O的半径为2，则等边△ABC的边长为（　　）

• A． 1
• B． $\sqrt{2}$
• C． $\sqrt{3}$
• D． $2\sqrt{3}$

Answer 1

分析 作OD⊥BC于D，连接OB，由垂径定理得出BD=CD=$\frac{1}{2}$BC，由等边三角形的性质和已知条件得出∠OBD=$\frac{1}{2}$∠ABC=30°，求出OD，再由三角函数求出BD，即可得出BC的长．

解答 解：作OD⊥BC于D，连接OB，如图所示：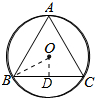
则BD=CD=$\frac{1}{2}$BC，
∵⊙O是等边三角形ABC的外接圆，
∴∠OBD=$\frac{1}{2}$∠ABC=30°，
∴OD=$\frac{1}{2}$OB=1，
∴BD=$\sqrt{3}$OD=$\sqrt{3}$，
∴BC=2BD=2$\sqrt{3}$，
即等边△ABC的边长为2$\sqrt{3}$；
故选：D．

点评 本题考查了等边三角形的性质、垂径定理、含30°角的直角三角形的性质、三角函数；熟练掌握等边三角形的性质，并能进行推理计算是解决问题的关键．