题目内容
14. 如图,在Rt△ABD中,∠BDA=90°,AD=BD,点E在AD上,连接BE,将△BED绕点D顺时针旋转90°,得到△ACD,若∠BED=65°,则∠ACE的度数为( )
如图,在Rt△ABD中,∠BDA=90°,AD=BD,点E在AD上,连接BE,将△BED绕点D顺时针旋转90°,得到△ACD,若∠BED=65°,则∠ACE的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 先根据旋转的性质,得出△CDE是等腰直角三角形,且∠ACD=∠BED=65°,再根据角的和差关系,求得∠ACE的度数.
解答  解:由旋转可得,CD=ED,∠CDE=90°,∠ACD=∠BED=65°,
解:由旋转可得,CD=ED,∠CDE=90°,∠ACD=∠BED=65°,
∴△CDE是等腰直角三角形,
∴∠DCE=45°,
∴∠ACE=∠ACD-∠DCE=65°-45°=20°.
故选(B)
点评 本题主要考查了旋转的性质以及等腰直角三角形的性质,旋转前、后的图形全等,故对应角相等,对应边相等,这是解决问题的关键.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
4.不等式的解集x<-2在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
4.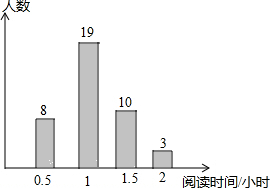 某中学组织了一次读书活动,随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中,阅读时间的中位数和众数分别是( )
某中学组织了一次读书活动,随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中,阅读时间的中位数和众数分别是( )
 某中学组织了一次读书活动,随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中,阅读时间的中位数和众数分别是( )
某中学组织了一次读书活动,随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中,阅读时间的中位数和众数分别是( )| A. | 2,1 | B. | 1,1.5 | C. | 1,2 | D. | 1,1 |
 如图,已知正方形ABCD,AB=4,动点M、N分别从D、B两点同时出发,且都以1个单位/秒的速度匀速运动,点M沿DA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥AD,交AC于点P,连结NP.设运动时间为x秒.
如图,已知正方形ABCD,AB=4,动点M、N分别从D、B两点同时出发,且都以1个单位/秒的速度匀速运动,点M沿DA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥AD,交AC于点P,连结NP.设运动时间为x秒.
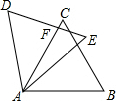 如图,将边长为6的等边三角形ABC绕点A逆时针旋转30度后得到△AED,边AC与DE交于点F,则AF的长为3$\sqrt{3}$.
如图,将边长为6的等边三角形ABC绕点A逆时针旋转30度后得到△AED,边AC与DE交于点F,则AF的长为3$\sqrt{3}$. 如图,△ABC是等腰直角三角形,AC=4,直线l垂直平分AC交AC于点D,点P在直线l上,求△APB的周长的最小值4+4$\sqrt{2}$.
如图,△ABC是等腰直角三角形,AC=4,直线l垂直平分AC交AC于点D,点P在直线l上,求△APB的周长的最小值4+4$\sqrt{2}$.