��Ŀ����
������8�֣���ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ������ÿ��С�����εı߳�Ϊ1����λ���ȣ�
��1����Ҫ����ͼ��
�ٻ�����ABC����ԭ��O�����ĶԳ�ͼ�Ρ�A1B1C1��
�ڻ�������ABC�Ƶ�A��ʱ����ת90��õ���AB2C2��
��2���ش��������⣺
�١�A1B1C1�ж���A1����Ϊ ������P��a��b��Ϊ��ABC����һ�㣬���գ�1���Т���ͼ����P��Ӧ�ĵ�P1������Ϊ ��
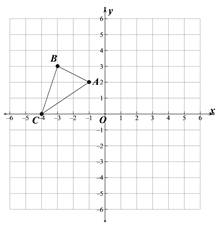
���𰸡���1����ͼ����������2����1��-2����-a,-b��
�������������������1�������ҳ���Ӧ���λ�ã���˳�����Ӽ��ɣ�
��2���ٸ���ͼ�ο�ֱ��д�����ꣻ�ڸ��ݹ���ԭ��ԳƵ�������ص�ɵô𰸣�
�����������1����ͼ��ʾ��
��2���ٸ���ͼ�οɵ�A1����Ϊ��2����4����
�ڵ�P1������Ϊ����a����b����
�ʴ�Ϊ������2����4��������a����b����
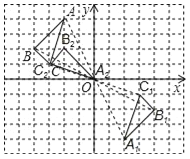
���㣺��ͼ-��ת�任��
�����͡������
��������
23
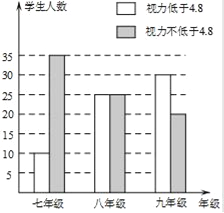
��ѧϰ�ˡ��ղ���������顱֮��ijУ�ˣ�1������ѧ��ȤС��Ը�Уѧ����������������˳������飬����������ͼ��ʾ������ͳ��ͼ�������ͼ����Ϣ����������⣺
��1�����γ���й������������ѧ����
��2����֪��У���꼶�����꼶�����꼶ѧ�����ֱ�Ϊ360�ˡ�400�ˡ�540�ˣ�
���Թ��㣺��У���꼶����������4.8��ѧ��Լ����������
�������æ�������У��������4.8��ѧ������
 ��������������������ϵ�д�
��������������������ϵ�д�

 �⣬��m��ȡֵ��Χ��_____��
�⣬��m��ȡֵ��Χ��_____�� ������˼����С������������̽����
������˼����С������������̽���� ������
������
 ��
�� ������С�����ҵ���һ�ְѲ���
������С�����ҵ���һ�ְѲ��� ��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
��ʽ�ӻ�Ϊƽ��ʽ�ķ����� ���ú�m��n��ʽ�ӷֱ��ʾ
���ú�m��n��ʽ�ӷֱ��ʾ


 ��(�� ������ ��
��(�� ������ �� ����
���� ��
��
 ��
�� ����C��D���㣮
����C��D���㣮

 ��
�� ���Ժϲ�����a��ֵ��_____.
���Ժϲ�����a��ֵ��_____. ����2��(2x��y)2��(2x��y)(2x��y)
����2��(2x��y)2��(2x��y)(2x��y) �����壬��x��ȡֵ��Χ�ǣ� ��
�����壬��x��ȡֵ��Χ�ǣ� ��