题目内容
17.若规定f(x)是正整数x所唯一对应的实数,且对于任意的正整数a、b都有f(a+b)=f(a)•f(b),如f(5)=f(3+2)=f(3)•f(2),现已知f(1)=$\sqrt{2}$.给出下列结论:①f(2)=2.
②若a>b,则必有f(a)>f(b).
③当a>b时,存在符合条件的a、b,使得2f(a)=f(a-b)+f(a+b)成立.
④当a>b时,必有f(2a)=f(a-b)•f(a+b)成立.
其中正确的结论是①②④(写出你认为正确的所有结论的序号).
分析 ①把2根据规定运算写成1+1代入即可得出结论正确;
②由于a>b,设a=b+n(n为整数)代入规定化简即可得出结论正确;
③根据规定f(a-b)+f(a+b)=0,再判断出f(a)≥$\sqrt{2}$,即可得出结论不正确;
④将f(a-b)•f(a+b)根据规定化简得出右边,即可判断出结论正确.
解答 解:①f(2)=f(1+1)=f(1)•f(1)=$\sqrt{2}×\sqrt{2}$=2,
∴①正确;
②设a=b+n,n为正整数,
∴f(a)=f(b)+f(n)=f(b)+nf(1)=f(b)+$\sqrt{2}$n>f(b),
∴②正确;
③∵f(a-b)+f(a+b)=-f(a)•f(b)+f(a)•f(b)=0,
由②知f(a)≥f(1),
∵f(1)=$\sqrt{2}$,
∴f(a)≥$\sqrt{2}$≠0,
∴③不正确;
④∵f(a-b)•f(a+b)=f(a-b+a+b)=f(2a),
∴④正确;
∴正确的有①②④
故答案为①②④.
点评 此题是实数运算,主要考查了学生的理解规定和运用规定的能力,是一道简单的新定义题目.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y=$\frac{k}{x}$(x>0)经过点C、G,则k=$\frac{7}{2}$.
如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y=$\frac{k}{x}$(x>0)经过点C、G,则k=$\frac{7}{2}$.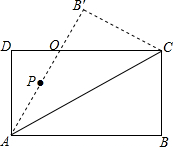 如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.
如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O. 已知:如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB、AC和CB的延长线于点D、E、F.求证:∠F+∠FEC=2∠A.
已知:如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB、AC和CB的延长线于点D、E、F.求证:∠F+∠FEC=2∠A. 如图,在△ABC中,点D、E在BC上,且∠1=∠B,∠2=∠C,BC=10cm,求△ADE的周长.
如图,在△ABC中,点D、E在BC上,且∠1=∠B,∠2=∠C,BC=10cm,求△ADE的周长. 如图,四边形PAOB是扇形OMN的内接矩形,顶点P在$\widehat{MN}$上,且不与M、N重合,当P点在$\widehat{MN}$上移动时,矩形PAOB的形状,大小随之变化,则AB的长度( )
如图,四边形PAOB是扇形OMN的内接矩形,顶点P在$\widehat{MN}$上,且不与M、N重合,当P点在$\widehat{MN}$上移动时,矩形PAOB的形状,大小随之变化,则AB的长度( )