题目内容
4．求下列各式的值：（1）cos260°-sin260°；
（2）$\frac{co{s}^{2}45°}{si{n}^{2}45°}$-tan45°；
（3）tan60°-2sin30°•cos30°；
（4）3tan30°-tan245°-2sin60°．
分析 根据特殊角三角函数值，可得答案．
解答 解：（1）cos260°-sin260°=（$\frac{1}{2}$）2-（$\frac{\sqrt{3}}{2}$）2=-$\frac{1}{2}$；
（2）$\frac{co{s}^{2}45°}{si{n}^{2}45°}$-tan45°=$\frac{（\frac{\sqrt{2}}{2}）^{2}}{（\frac{\sqrt{2}}{2}）^{2}}$-1=0；
（3）tan60°-2sin30°•cos30°=$\sqrt{3}$-2×$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$；
（4）3tan30°-tan245°-2sin60°=3×$\frac{\sqrt{3}}{3}$-1-2×$\frac{\sqrt{3}}{2}$=-1．
点评 本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键．
练习册系列答案
相关题目
14．已知A、B在数轴上分别表示的数为m、n．
（1）对照数轴完成下表：
（2）若A、B两点间的距离为d，试问d与m、n有何数量关系？
（3）已知A、B在数轴上分别表示的数为x和-2，则A、B两点的距离d可表示为d=|x+2|，如果d=3，求x的值．
（4）若数轴上表示数m的点位于-5和3之间，求|m+5|+|m-3|的值．
（1）对照数轴完成下表：
| m | 5 | -3 | -4 | -4 |
| n | 2 | 0 | 3 | -2 |
| A、B两点间的距离 | 3 | 3 | 7 | 2 |
（3）已知A、B在数轴上分别表示的数为x和-2，则A、B两点的距离d可表示为d=|x+2|，如果d=3，求x的值．
（4）若数轴上表示数m的点位于-5和3之间，求|m+5|+|m-3|的值．
甲、乙两人从A地出发，骑自行车在同一条路上行驶到B地，他们离出发地的距离s（千米）和行驶时间t（时）之间的关系的图象如图所示．根据图中提供的信息，有下列说法：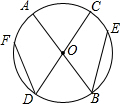
如图，AB，CD是⊙O的直径，DF，BE是弦，且DF=BE，求证：$\widehat{AF}$=$\widehat{CE}$．
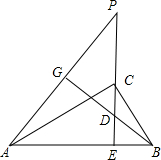如图，CE是直角△ABC斜边AB上的高，在EC的延长线上任取一点P，连接AP，过B作BG⊥AP于G，交CE于D，求证：CE2=PE•DE．
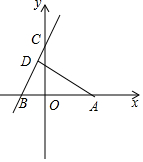如图，在直角坐标系xOy中，点A（2，0）和点B（-2，0），直线BC与y轴正半轴交于点C（0，b），过点A作AD⊥BC，垂足为D，联结OD．