题目内容
16.①化简:(xy-y2)$÷\frac{x-y}{xy}$②化简并求值$\frac{2a}{{a}^{2}-4}-\frac{1}{a+2}$,然后从2,-2,3中任选一个你喜欢的a的值代入求值.
分析 ①原式利用除法法则变形,约分即可得到结果;
②原式通分并利用同分母分式的减法法则计算,约分得到最简结果,把a=3代入计算即可求出值.
解答 解:①原式=y(x-y)•$\frac{xy}{x-y}$
=xy2;
②原式=$\frac{2a}{(a+2)(a-2)}$-$\frac{a-2}{(a+2)(a-2)}$
=$\frac{2a-a+2}{(a+2)(a-2)}$
=$\frac{1}{a-2}$,
当a=3时,原式=1.
点评 此题考查了分式的化简求值,以及分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.计算(a3)3÷(-a2)4的结果是( )
| A. | a4 | B. | a3 | C. | a2 | D. | a |
8.已知抛物线y=ax2-2ax-a+1的顶点在x轴上,则a的值是( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 1 |
6.下列式子成立的是( )
| A. | $\frac{1}{\sqrt{3}}$=$\sqrt{3}$ | B. | 2$\sqrt{3}$-$\sqrt{3}$=2 | C. | $\sqrt{(-3)^{2}}$=3 | D. | ($\sqrt{3}$)2=6 |
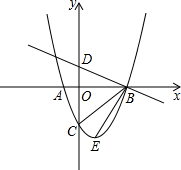 如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线$y=-\frac{1}{3}x+1$与y轴交于点D.求∠DBC-∠CBE.
如图,抛物线y=ax2+bx-3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.直线$y=-\frac{1}{3}x+1$与y轴交于点D.求∠DBC-∠CBE.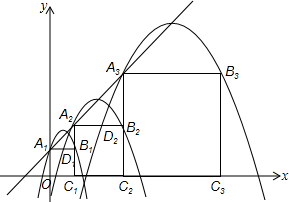 在平面直角坐标系中xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3…、An和点C1,C2,C3…、Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1、B1,且顶点在直线y=x+1上,抛物线L2过点A2、B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An、Bn,且顶点也在直线y=x+1上,其中抛物线L1交正方形A1B1C1O的边A1B1于点D1,抛物线L2交正方形A2B2C2C1的边A2B2于点D2…,抛物线Ln交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).
在平面直角坐标系中xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3…、An和点C1,C2,C3…、Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1、B1,且顶点在直线y=x+1上,抛物线L2过点A2、B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An、Bn,且顶点也在直线y=x+1上,其中抛物线L1交正方形A1B1C1O的边A1B1于点D1,抛物线L2交正方形A2B2C2C1的边A2B2于点D2…,抛物线Ln交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).