题目内容
3. 如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=$\frac{2}{3}$,AB=12,求半圆O所在圆的半径.
分析 (1)根据等腰三角形的性质,可得OA,根据角平分线的性质,可得OE,根据切线的判定,可得答案;
(2)根据余弦,可得OB的长,根据勾股定理,可得OA的长,根据三角形的面积,可得OE的长.
解答 (1)证明:如图1 ,
,
作OD⊥AC于D,OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC于D,OE⊥AB于E,
∴OD=OE,
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线;
(2)cos∠ABC=$\frac{2}{3}$,AB=12,得
OB=8.
由勾股定理,得
AO=$\sqrt{A{B}^{2}-O{B}^{2}}$=4$\sqrt{5}$.
由三角形的面积,得
S△AOB=$\frac{1}{2}$AB•OE=$\frac{1}{2}$OB•AO,
OE=$\frac{OB•AO}{AB}$=$\frac{8\sqrt{5}}{3}$,
半圆O所在圆的半径是$\frac{8\sqrt{5}}{3}$.
点评 本题考查了切线的判定与性质,利用切线的判定是解题关键,利用面积相等得出关于OE的长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.(x2y)3的结果是( )
| A. | x5y3 | B. | x6y | C. | 3x2y | D. | x6y3 |
18.下列命题中错误的是( )
| A. | 两组对角分别相等的四边形是平行四边形 | |
| B. | 矩形的对角线相等 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
8. 如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )
如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )
 如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )
如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
17.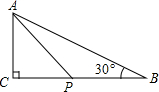 如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
 如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )| A. | 3 | B. | 3.5 | C. | 4.8 | D. | 5.2 |