题目内容
12.计算2$\sqrt{\frac{1}{2}}$-$\sqrt{18}$的结果是-2$\sqrt{2}$.分析 先将各个二次根式化成最简二次根式,再把同类二次根式进行合并求解即可.
解答 解:原式=2×$\frac{\sqrt{2}}{2}$-3$\sqrt{2}$
=$\sqrt{2}$-3$\sqrt{2}$
=-2$\sqrt{2}$,
故答案为:-2$\sqrt{2}$.
点评 本题考查了二次根式的加减法,解答本题的关键在于掌握二次根式的化简与同类二次根式合并.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
2.某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
| “读书节”活动计划书 | ||
| 书本类别 | A类 | B类 |
| 进价(单位:元) | 18 | 12 |
| 备注 | 1、用不超过16800元购进A、B两类图书共1000本; 2、A类图书不少于600本; … | |
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
3. 如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=$\frac{2}{3}$,AB=12,求半圆O所在圆的半径.
 如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=$\frac{2}{3}$,AB=12,求半圆O所在圆的半径.
20.某种细胞的直径是0.00000095米,将0.00000095米用科学记数法表示为( )
| A. | 9.5×10-7 | B. | 9.5×10-8 | C. | 0.95×10-7 | D. | 95×10-8 |
7.-6的绝对值是( )
| A. | -6 | B. | 6 | C. | $\frac{1}{6}$ | D. | -$\frac{1}{6}$ |
1.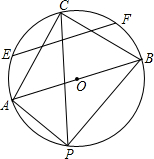 如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是( )
如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是( )
 如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是( )
如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是( )| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 6 | D. | 2$\sqrt{5}$ |
8. 如图,已知点D、E分别在△ABC边AB、AC上,DE∥BC,BD=2AD,那么S△DBE:S△EBC等于( )
如图,已知点D、E分别在△ABC边AB、AC上,DE∥BC,BD=2AD,那么S△DBE:S△EBC等于( )
 如图,已知点D、E分别在△ABC边AB、AC上,DE∥BC,BD=2AD,那么S△DBE:S△EBC等于( )
如图,已知点D、E分别在△ABC边AB、AC上,DE∥BC,BD=2AD,那么S△DBE:S△EBC等于( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:# |
 如图,已知一次函数y=ax-2的图象与反比例函数y=$\frac{k}{x}$的图象交于A(k,a),B两点.
如图,已知一次函数y=ax-2的图象与反比例函数y=$\frac{k}{x}$的图象交于A(k,a),B两点.