题目内容
2.在平面直角坐标中,A(-2,0),B(0,2),C(2,0).(1)如图①,BD∥AC,且AD=AC,求点D的坐标;
(2)如图②,将线段OC绕O点旋转至OE,当点E在第四象限时,请探究:线段AE,BE,CE之间的数量关系;
(3)如图③,将线OC绕O点旋转至OE,当E在第一象限时,..直接写出线段AE,BE,CE之间的数量关系为AE-CE=$\sqrt{2}$BE.
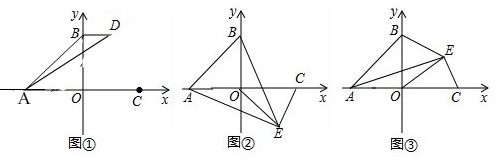
分析 (1)设出点D的坐标,用两点间的距离公式得出AD,AC,最后用AD=AC建立方程求解即可;
(2)先判断出△ABC是等腰直角三角形,再判断出∠AEC=90°=∠ABC,进而得出点A,B,C,E四点共圆,即可得出∠BCF=∠BAE,即可判断出△ABE≌△CBF,得出AE=CF,再用勾股定理得出EF=$\sqrt{2}$BE,最后代换即可得出结论;
(3)同(2)的方法即可得出结论.
解答 解:(1)∵A(-2,0),C(2,0).
∴AC=4,
∵BD∥AC,B(0,2),
∴设D(m,2),
∵A(-2,0),
∴AD=$\sqrt{(m+2)^{2}+4}$,
∵AD=AC,
∴$\sqrt{(m+2)^{2}+4}$=4,
∴m=-2±2$\sqrt{3}$,
∴D(-2-2$\sqrt{3}$,2)或D(-2+2$\sqrt{3}$,2);
(2)AE+CE=$\sqrt{2}$BE;
理由:如图1,连接BC,过点B作BF⊥BE交EC延长线于F, ∵A(-2,0),B(0,2),C(2,0),
∵A(-2,0),B(0,2),C(2,0),
∴OA=OB=OC=2,
∵OB⊥AC,
∴△ABC是等腰直角三角形,
∵线段OC绕O点旋转至OE,
∴OE=OA=OC
∴△ACE是直角三角形,
∴∠AEC=90°=∠ABC,
∴点A,B,C,E四点共圆,
∴∠BCF=∠BAE,
∵∠ABC=∠EBF=90°,
∴∠ABE=∠CBF,
在△ABE和△CBF中,$\left\{\begin{array}{l}{∠ABE=∠CBF}\\{AB=BC}\\{∠BAE=∠BCF}\end{array}\right.$,
∴△ABE≌△CBF,
∴AE=CF,
在R△EBF中,∠BEF=∠BAC=45°,
∴EF=$\sqrt{2}$BE,
∵EF=CE+CF=CE+AE,
∴AE+CE=$\sqrt{2}$BE;
(3)AE-CE=$\sqrt{2}$BE,
理由:如图2, 连接BC,过点B作BF⊥BE交AE于F,
连接BC,过点B作BF⊥BE交AE于F,
同(2)的方法,得△BCE≌△BAF,
∴CE=AF,
在R△EBF中,∠BEF=∠BAC=45°,
∴EF=$\sqrt{2}$BE,
∵EF=AE-AF=AE-CE,
∴AE-CE=$\sqrt{2}$BE,
故答案为:AE-CE=$\sqrt{2}$BE.
点评 此题是三角形综合题,主要考查了平面坐标系内,两点间的距离公式,等腰直角三角形的判定和性质,四点共圆,全等三角形的判断和性质,勾股定理;解(1)的关键是用AD=AC,建立方程$\sqrt{(m+2)^{2}+4}$=4,解(2)(3)关键是△ABE≌△CBF,是一道中等难度的中考常考题.

 阅读快车系列答案
阅读快车系列答案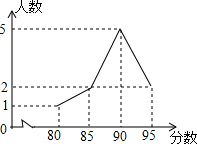 在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )
在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )| A. | 88 | B. | 89 | C. | 90 | D. | 91 |
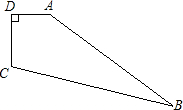 如图,在四边形ABCD中,∠D=90°,AD=3,DC=4,AB=12,BC=13.求四边形ABCD的面积.
如图,在四边形ABCD中,∠D=90°,AD=3,DC=4,AB=12,BC=13.求四边形ABCD的面积.
 如图是一个正方体的平面展开图,相对面上的两个数之和均为5,求x+y+z=4.
如图是一个正方体的平面展开图,相对面上的两个数之和均为5,求x+y+z=4.