题目内容
4.已知|x+1|+(2y-3)2014=0,则x+y=$\frac{1}{2}$.分析 直接利用偶次方的性质以及绝对值的性质得出x,y的值,进而得出答案.
解答 解:∵|x+1|+(2y-3)2014=0,
∴x+1=0,2y-3=0,
解得:x=-1,y=$\frac{3}{2}$,
则x+y=-1+$\frac{3}{2}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题主要考查了偶次方的性质以及绝对值的性质,得出x,y的值是解题关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
15.从下列不等式中选择一个与x+2≥2组成不等式组,若要使该不等式组的解集为x≥1,则可以选择的不等式是( )
| A. | x≥1 | B. | x>2 | C. | x<0 | D. | x<2 |
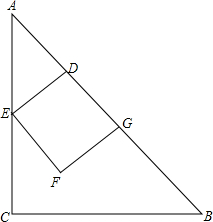 如图,在Rt△ABC中,∠ACB=90°,CA=CB=6,动点D从点A出发沿AB以每秒$\sqrt{2}$个单位的速度向点B运动,到达点B时停止运动,过点D作AB的垂线交折线AC-BC于点E,以DE为边向下作正方形DEFG,点G在AB上,正方形DEFG与△ABC重叠部分的面积为y,动点D运动的时间为t.
如图,在Rt△ABC中,∠ACB=90°,CA=CB=6,动点D从点A出发沿AB以每秒$\sqrt{2}$个单位的速度向点B运动,到达点B时停止运动,过点D作AB的垂线交折线AC-BC于点E,以DE为边向下作正方形DEFG,点G在AB上,正方形DEFG与△ABC重叠部分的面积为y,动点D运动的时间为t.