题目内容
19.若[x]表示不超过x的最大整数(如[π]=3,[-2$\frac{2}{3}$]=-3等),求[$\frac{1}{2-\sqrt{1×2}}$]+[$\frac{1}{3-\sqrt{2×3}}$]+…+[$\frac{1}{2015-\sqrt{2014×2015}}$]的值.分析 根据已知得出[$\frac{1}{2-\sqrt{1×2}}$]=[$\frac{2+\sqrt{2}}{2}$]=[1+$\frac{\sqrt{2}}{2}$]=1,[$\frac{1}{3-\sqrt{2×3}}$]=[$\frac{3+\sqrt{6}}{3}$]=1,…[$\frac{1}{2015-\sqrt{2014×2015}}$]=$\frac{2015+\sqrt{2014×2015}}{2015}$]=1,进而求出即可.
解答 解:∵[x]表示不超过x的最大整数,
∴[$\frac{1}{2-\sqrt{1×2}}$]+[$\frac{1}{3-\sqrt{2×3}}$]+…+[$\frac{1}{2015-\sqrt{2014×2015}}$]
=[$\frac{2+\sqrt{2}}{2}$]+[$\frac{3+\sqrt{6}}{3}$]+…+$\frac{2015+\sqrt{2014×2015}}{2015}$]
=1+1+…+1
=2014.
点评 此题主要考查了取整计算,正确利用二次根式的性质化简已知式子是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
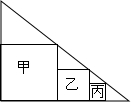 如图,一直角三角形中有三个连续排列的正方形甲、乙、丙,已知正方形甲、乙的边长分别为9、6,求正方形丙的边长.
如图,一直角三角形中有三个连续排列的正方形甲、乙、丙,已知正方形甲、乙的边长分别为9、6,求正方形丙的边长.