题目内容
14.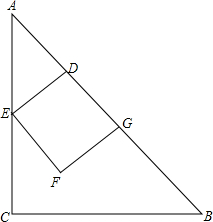 如图,在Rt△ABC中,∠ACB=90°,CA=CB=6,动点D从点A出发沿AB以每秒$\sqrt{2}$个单位的速度向点B运动,到达点B时停止运动,过点D作AB的垂线交折线AC-BC于点E,以DE为边向下作正方形DEFG,点G在AB上,正方形DEFG与△ABC重叠部分的面积为y,动点D运动的时间为t.
如图,在Rt△ABC中,∠ACB=90°,CA=CB=6,动点D从点A出发沿AB以每秒$\sqrt{2}$个单位的速度向点B运动,到达点B时停止运动,过点D作AB的垂线交折线AC-BC于点E,以DE为边向下作正方形DEFG,点G在AB上,正方形DEFG与△ABC重叠部分的面积为y,动点D运动的时间为t.(1)求AB的长;
(2)当t为何值时,点E落在点C?当t为何值时,点F落在BC上?
(3)当E在线段AC上时,求DF的长(用含t的式子表示);
(4)求y与t的函数关系式.
分析 (1)利用勾股定理求得AB的长即可;
(2)当点E落在点C处时,由等腰三角形三线合一的性质即可求得t的取值范围;根据等腰直角三角形的性质和正方形的性质进行证明即可;
(3)根据△ADE是等腰直角三角形以及勾股定理进行解答即可;
(4)如图2所示,重合部分的面积=正方形的面积;如图3所示,重合部分的面积=正方形的面积-三角形的面积.
解答 解:(1)由勾股定理得AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$;
(2)当点E与点C重合时,
∵DE⊥AB,AC=CB,
∴AD=BD.
∴AD=$\frac{1}{2}$AB=3$\sqrt{2}$.
∴t=3.
当点F落在BC上时,如图1所示.
∵△AED和△BGF为等腰直角三角形,四边形DEFG为正方形,
∴AD=DG=GB.
∴t=$\frac{1}{3}$AB=2$\sqrt{2}$.
(3)根据题意可知:△AED为等腰直角三角形,四边形DEFG为正方形.
∴DE=EF=AD=t.
在△DEF中,由勾股定理可知:DF=$\sqrt{D{E}^{2}+E{F}^{2}}$=$\sqrt{{t}^{2}+{t}^{2}}$=$\sqrt{2}t$.
(4)如图2所示:
重合部分的面积=正方形DEFG的面积.
∴y=t2(0<t<$\frac{2\sqrt{6}}{3}$).
如图3所示;
∵△ADE为等腰直角三角形,
∴AD=ED=t.
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{2}t$.
∴EC=6-$\sqrt{2}t$.
根据题意可知△ECM为等腰直角三角形,
∴CM=EC=6-$\sqrt{2}t$.
在△CEM中,由勾股定理得:ME=$\sqrt{C{E}^{2}+C{M}^{2}}$=6$\sqrt{2}$-2t.
∴MF=EF-EM=t-(6$\sqrt{2}$-2t)=3t-6$\sqrt{2}$.
∴△MNF的面积=$\frac{1}{2}MF•FN=\frac{1}{2}×(3t-6\sqrt{2})^{2}$.
∵重合部分的面积=正方形的面积-△FMN的面积,
∴y=${t}^{2}-\frac{1}{2}(3t-6\sqrt{2})^{2}$=$-\frac{7}{2}{t}^{2}+18\sqrt{2}t-36$.
综上所述,y与t的函数关系式为y=$\left\{\begin{array}{l}{{t}^{2}(0<t<\frac{2\sqrt{6}}{3})}\\{-\frac{7}{2}{t}^{2}+18\sqrt{2}t-36(\frac{2\sqrt{6}}{3}<t<6)}\end{array}\right.$.
点评 本题主要考查的是正方形的性质、等腰直角三角形的性质、勾股定理的应用,根据题意画出符合题意的图形是解题的关键.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 的卡片,那么加上卡片上的数字,如果抽到形如
的卡片,那么加上卡片上的数字,如果抽到形如 的卡片,那么减去卡片上的数字,
的卡片,那么减去卡片上的数字,

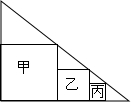 如图,一直角三角形中有三个连续排列的正方形甲、乙、丙,已知正方形甲、乙的边长分别为9、6,求正方形丙的边长.
如图,一直角三角形中有三个连续排列的正方形甲、乙、丙,已知正方形甲、乙的边长分别为9、6,求正方形丙的边长.