题目内容
1.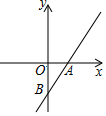 如图,直线y=kx+b与x轴交于点A(1,0),与 y交于点B(0,-2).
如图,直线y=kx+b与x轴交于点A(1,0),与 y交于点B(0,-2).(1)求直线AB的表达式;
(2)点C是直线AB上的点,且CA=AB,过动点P(m,0)且垂直于x轴的直线与直线AB 交于点D,若点D不在线段BC上,写出m的取值范围.
分析 (1)把A、B的坐标代入函数解析式,即可求出k、b值,得出答案即可;
(2)求出C的坐标,结合图象和C的坐标得出即可.
解答 解:(1)将 A(1,0),B(0,-2)代入y=kx+b得:$\left\{\begin{array}{l}{k+b=0}\\{b=-2}\end{array}\right.$,
解得:b=-2,k=2,
所以直线AB的表达式是y=2x-2;
(2)过点C 作CE⊥x 轴,垂足是E,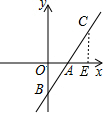
∵CA=AB,
∠BOA=∠AEC=90°,
∠BOA=∠CAE,
∴△BOA≌△CAE,
∴CE=AB=2,AE=OA=1,
∴C(2,2),
由图示知,m<0或 m>2.
点评 本题考查了坐标与图形性质,全等三角形的性质和判定,用待定系数法求函数的解析式等知识点,能求出函数的解析式和C的坐标是解此题的关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
18. 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )| A. | AB=AD | B. | BC=CD | C. | $\widehat{AB}=\widehat{AD}$ | D. | ∠BCA=∠DCA |
12.由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
| 售价(元/台) | 月销售量(台) |
| 400 | 200 |
| 390 | 250 |
| x | -5x+2200 |
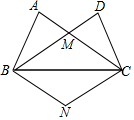 如图,在△ABC和△BCD中,AB=DC,AC=DB,AC、DB交于点M.
如图,在△ABC和△BCD中,AB=DC,AC=DB,AC、DB交于点M.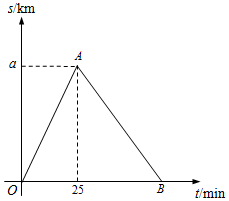 某市举行“迷你马拉松”长跑比赛,运动员从起点甲地出发,跑到乙地后,沿原路线再跑回点甲地.设该运动员离开起点甲地的路程s(km)与跑步时间t(min)之间的函数关系如图所示.已知该运动员从甲地跑到乙地时的平均速度是0.2km/min,根据图象提供的信息,解答下列问题:
某市举行“迷你马拉松”长跑比赛,运动员从起点甲地出发,跑到乙地后,沿原路线再跑回点甲地.设该运动员离开起点甲地的路程s(km)与跑步时间t(min)之间的函数关系如图所示.已知该运动员从甲地跑到乙地时的平均速度是0.2km/min,根据图象提供的信息,解答下列问题: