题目内容
11.不等式组$\left\{\begin{array}{l}{\frac{1}{2}x≤1}\\{2-x<3}\end{array}\right.$的整数解的和是3.分析 首先解每个不等式,两个不等式的公共部分就是不等式组的解集,确定解集中的整数解,然后求和即可.
解答 解:$\left\{\begin{array}{l}{\frac{1}{2}x≤1…①}\\{2-x<3…②}\end{array}\right.$,
解①得x≤2,
解②得x>-1,
则不等式组的解集是-1<x≤2.
则整数解是0,1,2.
整数解的和是3.
故答案是:3.
点评 此题考查了一元一次不等式组的整数解,以及一元一次不等式组的解法,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
3.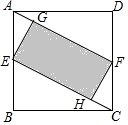 如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
 如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )| A. | y=3$\sqrt{3}$x2 | B. | y=4$\sqrt{3}$x2 | C. | y=8x2 | D. | y=9x2 |
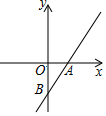 如图,直线y=kx+b与x轴交于点A(1,0),与 y交于点B(0,-2).
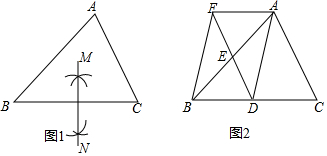
如图,直线y=kx+b与x轴交于点A(1,0),与 y交于点B(0,-2). 如图,在△ABC中,AB=AC=4,∠C=72°,D是AB的中点,点E在AC上,DE⊥AB,则∠ABE的度数为36°.
如图,在△ABC中,AB=AC=4,∠C=72°,D是AB的中点,点E在AC上,DE⊥AB,则∠ABE的度数为36°. 如图,圆锥的底面半径为9cm,母线长为30cm,这个圆锥的侧面积为270πcm2.
如图,圆锥的底面半径为9cm,母线长为30cm,这个圆锥的侧面积为270πcm2.
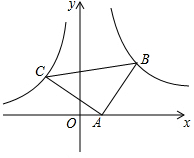 如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点C在双曲线y=-$\frac{4}{x}$(x<0)上,点A在x轴的正半轴上,且△ABC是以BC为斜边的等腰直角三角形.
如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点C在双曲线y=-$\frac{4}{x}$(x<0)上,点A在x轴的正半轴上,且△ABC是以BC为斜边的等腰直角三角形.