题目内容
8.二次函数y=2(m+1)(x-m)2的对称轴是y轴,则m的值是0,抛物线的顶点坐标是(0,0).分析 由二次函数的解析式可求得抛物线的对称轴,可得到关于m的方程,可求得m的值,进一步可求得顶点坐标.
解答 解:
∵y=2(m+1)(x-m)2,
∴抛物线对称轴为x=m,顶点坐标为(m,0),
∵对称轴是y轴,
∴m=0,顶点坐标为(0,0),
故答案为:0;(0,0).
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,其对称轴为x=h,顶点坐标为(h,k).

练习册系列答案
相关题目
16.下列命题中,是真命题的是( )
| A. | 内错角相等 | |
| B. | 同位角互补,两直线平行 | |
| C. | 一个角的余角不等于其自身 | |
| D. | 在同一平面内,过一点能作且只能作一条直线与已知直线垂直 |
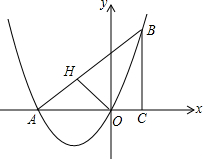 如图,在△ABC中,∠ACB=90°,BC=3,AC=3,将∠ABC对折,使点C的对应点H恰好落在直线AB上,折痕交AC于点O,以点O为坐标原点,AC所在直线为x轴建立平面直角坐标系,抛物线经过A、B、O三点.
如图,在△ABC中,∠ACB=90°,BC=3,AC=3,将∠ABC对折,使点C的对应点H恰好落在直线AB上,折痕交AC于点O,以点O为坐标原点,AC所在直线为x轴建立平面直角坐标系,抛物线经过A、B、O三点.