Question

13．如图，在平面直角坐标系中，直线y=-x+3与x轴，y轴分别交于点B、C；抛物线y=-x²+bx+c经过B、C两点，并与x轴交于另一点A．
（1）求该抛物线所对应的函数关系式；
（2）若点D是该抛物线对称轴上的一个动点，求△DAC周长的最小值；
（3）设P（x，y）是（1）所得抛物线上的一个动点，过点P作直线l⊥x轴于点M，交直线BC于点N．
①若点P在第一象限内，试问：线段PN的长度是否存在最大值？若存在，求出它的最大值及此时x的值；若不存在，请说明理由；
②求以BC为底边的等腰△BPC的面积．

Answer 1

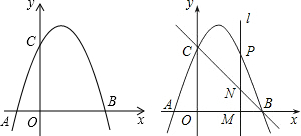
分析 （1）利用一次函数与坐标轴坐标求法，得出B、C两点的坐标，利用待定系数法求出二次函数解析式．
（2）如图1中，连接CB交对称轴于P，此时△PAC的周长最小．
（3）①设点P的坐标为（x，-x²+2x+3），则N的坐标为（x，-x+3），构建二次函数，然后由二次函数的最值问题，求得答案；
②求出BC的垂直平分线的解析式，用方程组求出点P的坐标即可解决问题．

解答 解：（1）由于直线y=-x+3经过B、C两点，
令y=0得x=3；令x=0，得y=3，
∴B（3，0），C（0，3），
∵点B、C在抛物线y=-x²+bx+c上，于是得
$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=3}\end{array}\right.$，
解得b=2，c=3，
∴所求函数关系式为y=-x²+2x+3；

（2）如图1中，连接CB交对称轴于P，此时△PAC的周长最小．

∵A（-1，0），C（0，3），B（3，0），
∴AC=$\sqrt{10}$，BC=3$\sqrt{2}$，
∴△PAC的周长的最小值=AC+PA+PC=AC+PB+PC=AC+BC=$\sqrt{10}$+3$\sqrt{2}$．

（3）①如图2中，

∵点P（x，y）在抛物线y=-x²+2x+3上，
且PN⊥x轴，
∴设点P的坐标为（x，-x²+2x+3），
同理可设点N的坐标为（x，-x+3），
又点P在第一象限，
∴PN=PM-NM，
=（-x²+2x+3）-（-x+3），
=-x²+3x，
=-（x-$\frac{3}{2}$）²+$\frac{9}{4}$，
∴当x=$\frac{3}{2}$时，
线段PN的长度的最大值为 $\frac{9}{4}$．
②解：如图3中，

由题意知，点P在线段BC的垂直平分线上，
又由①知，OB=OC，
∴BC的中垂线同时也是∠BOC的平分线，
∴设点P的坐标为（a，a），
又点P在抛物线y=-x²+2x+3上，于是有a=-a²+2a+3，
∴a²-a-3=0，
解得a1=$\frac{1+\sqrt{13}}{2}$，a2=$\frac{1-\sqrt{13}}{2}$，
∴点P的坐标为：（ $\frac{1+\sqrt{13}}{2}$，$\frac{1+\sqrt{13}}{2}$）或（ $\frac{1-\sqrt{13}}{2}$，$\frac{1-\sqrt{13}}{2}$），
若点P的坐标为（ $\frac{1+\sqrt{13}}{2}$，$\frac{1+\sqrt{13}}{2}$），此时点P在第一象限，
在Rt△OMP和Rt△BOC中，MP=OM=$\frac{1+\sqrt{13}}{2}$，
OB=OC=3，
S_△BPC=S_{四边形BOCP}-S_△BOC=2S_△BOP-S_△BOC=2×$\frac{1}{2}$•BO•PM-$\frac{1}{2}$BO•CO，
=2×$\frac{1}{2}$×3×$\frac{1+\sqrt{13}}{2}$-$\frac{9}{2}$，
=$\frac{3\sqrt{3}-6}{2}$，
若点P的坐标为（ $\frac{1-\sqrt{13}}{2}$，$\frac{1-\sqrt{13}}{2}$），此时点P在第三象限，
则S_△BPC=S_△BOP+S_△COP+S_△BOC=$\frac{1}{2}$×3×|$\frac{1-\sqrt{13}}{2}$|×2+$\frac{1}{2}$×3×3=$\frac{3\sqrt{13}+6}{2}$．
综上所述△BPC的面积为$\frac{3\sqrt{13}-6}{2}$或$\frac{3\sqrt{13}+6}{2}$．

点评 此题主要考查了待定系数法求二次函数解析式，线段垂直平分线的性质，二次函数最值问题，解题的关键是学会利用对称解决最小值问题，学会构建二次函数解决最值问题，属于中考压轴题．