题目内容
3.计算:$\sqrt{32+4\sqrt{7}+2\sqrt{3}+4\sqrt{21}}$×($\sqrt{3}$-1)=2+2$\sqrt{21}$-2$\sqrt{7}$.分析 先利用完全平方公式把前面的复合二次根式进行化简,然后进行二次根式的乘法运算.
解答 解:原式=$\sqrt{4+2\sqrt{3}+28+(\sqrt{3}+1)•4\sqrt{7}}$×($\sqrt{3}$-1)
=$\sqrt{(\sqrt{3}+1)^{2}+2×(\sqrt{3}+1)×2\sqrt{7}+(2\sqrt{7})^{2}}$×($\sqrt{3}$-1)
=$\sqrt{(\sqrt{3}+1+2\sqrt{7})^{2}}$×($\sqrt{3}$-1)
=($\sqrt{3}$+1+2$\sqrt{7}$)($\sqrt{3}$-1)
=($\sqrt{3}$+1)($\sqrt{3}$-1)+2$\sqrt{7}$($\sqrt{3}$-1)
=3-1+2$\sqrt{21}$-2$\sqrt{7}$
=2+2$\sqrt{21}$-2$\sqrt{7}$.
故答案为2+2$\sqrt{21}$-2$\sqrt{7}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
13.下面图案中是轴对称图形的有( )

| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
 已知钝角△ABC,试画出:
已知钝角△ABC,试画出: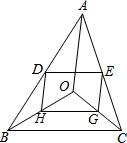 如图,在△ABC中,D、E分别是边AB、AC的中点,O是三角形内部一点,连接OB、OC,G、H分别是OC、OB的中点,试说明四边形DEGH是平行四边形.
如图,在△ABC中,D、E分别是边AB、AC的中点,O是三角形内部一点,连接OB、OC,G、H分别是OC、OB的中点,试说明四边形DEGH是平行四边形.