题目内容
11. 正方形ABCD和正方形CEFG,连结BF,DF,点P为线段DF的中点,连接GP.
正方形ABCD和正方形CEFG,连结BF,DF,点P为线段DF的中点,连接GP.(1)如图1,如果点E,G分别在边BC、CD上,猜想BF与GP的数量关系,并给出证明;
(2)如图2,在如图1的基础上将正方形CEFG绕点C旋转,(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由.
分析 (1)根据正方形的性质得到DC=BC,CE=CG,FE=GF,∠DGF=∠FEB=90°,推出△BEF≌△DGF,由全等三角形的性质得到BF=DF,于是得到结论;
(2)延长FG到H,使GH=FG,连接CH,DH,CF,通过△BCF≌△DCH,得到BF=DH,根据三角形的中位线的性质即可得到结论.
解答 解:(1)∵四边形ABCD和CEFG是正方形,
∴DC=BC,CE=CG,FE=GF,∠DGF=∠FEB=90°,
∴BE=DG,
在△BEF和△DGF中
$\left\{\begin{array}{l}{BE=DG}\\{∠FEB=∠DGF}\\{EF=GF}\end{array}\right.$,
∴△BEF≌△DGF,
∴BF=DF,
∵P为线段DF的中点,
∴GP=$\frac{1}{2}$DF,
∴GP=$\frac{1}{2}$BF;
(2)成立,理由如下:
延长FG到H,使GH=FG,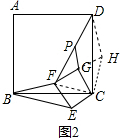 连接CH,DH,CF,
连接CH,DH,CF,
∵GH=FG=GC,CG⊥FH,
∴FC=HC,∠FCH=90°=∠BCD,
∴∠BCF=∠HCD,
在△BCF与△DCH中,$\left\{\begin{array}{l}{FC=HC}\\{∠BCF=∠HCD}\\{BC=DC}\end{array}\right.$,
∴△BCF≌△DCH,
∴BF=DH,
∵P,G分别是FD,FH的中点,
∴PG=$\frac{1}{2}$DH=$\frac{1}{2}$BF.
点评 本题考查了旋转的性质,全等三角形的判定和性质,三角形的中位线的性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目
6.一组按规律排列的式子:$\frac{2}{a}$,$\frac{5}{{a}^{2}}$,$\frac{10}{{a}^{3}}$,$\frac{17}{{a}^{4}}$,$\frac{26}{{a}^{5}}$…第n个式子是( )(用含n的式子表示,n为正整数)
| A. | $\frac{(n-1)^{2}}{{a}^{n}}$ | B. | $\frac{{n}^{2}-1}{{a}^{n}}$ | C. | $\frac{(n+1)^{2}}{{a}^{n}}$ | D. | $\frac{{n}^{2}+1}{{a}^{n}}$ |
20.某商店需要购进甲、乙两种商品共160件,其进价和售价如表:(注:获利=售价-进价)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2016次,点B的落点依次为B1,B2,B3,…,则B2016的坐标为(1344,$\sqrt{3}$).
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2016次,点B的落点依次为B1,B2,B3,…,则B2016的坐标为(1344,$\sqrt{3}$). 如图,已知点A、B、C是⊙O上的点,其中点C是弧AB的中点,OC=4cm,点P是OC延长线上一点,连接PA、PB.
如图,已知点A、B、C是⊙O上的点,其中点C是弧AB的中点,OC=4cm,点P是OC延长线上一点,连接PA、PB.