Question

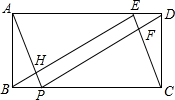如图：在矩形ABCD中，AB=2，BC=5，E、P分别在AD、BC上，且DE=BP=1．
求证：四边形EFPH为矩形．

Answer 1

考点：矩形的判定与性质

专题：证明题

分析：求出平行四边形APCE、DEBP，推出HP∥EF，HE∥FP，求出∠BEC=90°，根据矩形的判定推出即可．

解答：证明：∵在矩形ABCD中，
∴AB=DC，AD∥BC，
∵ED=BP，
∴四边形DEBP是平行四边形，
∴BE∥DP，
∵AD=BC，AD∥BC，DE=BP，∴AE=CP，
∴四边形AECP是平行四边形，
∴AP∥CE，
∴四边形EFPH是平行四边形，
∵在矩形ABCD中，
∴∠ADC=∠ABP=90°，AD=BC=5，AB=CD=2，
∴CE=

5

，同理BE=2

5

，
∴BE²+CE²=BC²
∴∠BEC=90°，
∴四边形EFPH是矩形．

点评：本题考查了矩形的性质和判定，平行四边形的性质和判定，勾股定理的逆定理的应用，解此题的关键是求出四边形HPFE是平行四边形和求出∠BEC=90°．