题目内容
 如图所示,点E在AC上,∠1=∠2,∠3=∠4,试说明:BE=DE.
如图所示,点E在AC上,∠1=∠2,∠3=∠4,试说明:BE=DE.考点:全等三角形的判定与性质
专题:证明题
分析:根据ASA推出△ABC≌△ADC,根据全等三角形的性质得出BC=CD,根据SAS推出△BCE≌△DCE,根据全等三角形的性质推出即可.
解答:
解:∵在△ABC和△ADC中
,
∴△ABC≌△ADC(ASA),
∴BC=CD,
在△BCE和△DCE中,
,
∴△BCE≌△DCE(SAS),
∴BE=DE.
|
∴△ABC≌△ADC(ASA),
∴BC=CD,
在△BCE和△DCE中,
|
∴△BCE≌△DCE(SAS),
∴BE=DE.
点评:本题考查了全等三角形的性质和判定的应用,能正确运用定理进行推理是解此题的关键,注意:全等三角形的判定定理有:SAS,ASA,AAS,SSS,全等三角形的对应角相等,对应边相等.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
在数轴上,0为原点,某点A移动到B,移动了12.6个单位长度;点A表示数a,点B表示数b,且a+b=0,A到0的距离为( )
| A、12.6 | B、6.3 |
| C、-12.6 | D、-6.3 |
将抛物线y=ax2-1(a≠0)的图象向左平移2个单位后,所得抛物线经过(1,-4)点,则a等于( )
A、-
| ||
| B、-1 | ||
| C、-3 | ||
| D、-5 |
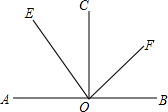 如图,A,O,B在一条直线上,OC是射线,OE平分∠AOC,OF平分∠BOC.
如图,A,O,B在一条直线上,OC是射线,OE平分∠AOC,OF平分∠BOC.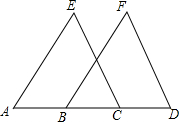 已知:如图,点A、B、C、D在同一条直线上,AE∥BF,AE=BF,AB=CD.求证:CE∥DF.
已知:如图,点A、B、C、D在同一条直线上,AE∥BF,AE=BF,AB=CD.求证:CE∥DF. 已知a,b,c三个数在数轴上的对应点如图所示,求|c-b|-|a-c|+
已知a,b,c三个数在数轴上的对应点如图所示,求|c-b|-|a-c|+ 已知B,A,D在同一条直线上,∠1=∠C,∠B=40°,求∠BAE的度数.
已知B,A,D在同一条直线上,∠1=∠C,∠B=40°,求∠BAE的度数.