题目内容
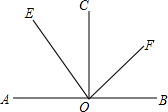 如图,A,O,B在一条直线上,OC是射线,OE平分∠AOC,OF平分∠BOC.
如图,A,O,B在一条直线上,OC是射线,OE平分∠AOC,OF平分∠BOC.(1)OE与OF有什么位置关系?为什么?
(2)如果射线OC绕点O旋转(在同一平面内).其他条件不变,那么(1)中的结论还成立吗?由此你能得到什么结论?
考点:角平分线的定义,角的计算
专题:
分析:(1)根据平角和角平分线的定义即可求出OE与OF的位置关系;
(2)邻补角的两角的平分线互相垂直.
(2)邻补角的两角的平分线互相垂直.
解答:
解:(1)OD与OE的位置关系是互相垂直.理由如下:
∵OE平分∠AOC,OF平分∠BOC,
∴∠EOC+∠COF=
∠AOC+∠BOC=
(∠AOC+∠BOC)=90°,
∴OD与OE的位置关系是互相垂直;
(2)结论仍成立.
因为无论OC如何旋转,始终符合以下关系
∠EOC=
∠AOC,FOC=
∠BOC,
∠EOF=
(∠AOC+∠BOC)=90°,
所以结论仍成立.
由此得到:邻补角的两角的平分线互相垂直.
∵OE平分∠AOC,OF平分∠BOC,
∴∠EOC+∠COF=
| 1 |
| 2 |
| 1 |
| 2 |
∴OD与OE的位置关系是互相垂直;
(2)结论仍成立.
因为无论OC如何旋转,始终符合以下关系
∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
∠EOF=
| 1 |
| 2 |
所以结论仍成立.
由此得到:邻补角的两角的平分线互相垂直.
点评:此题综合考查角平分线,余角,要记住互为余角的两个角的和为90度.同时考查了垂直的判定.

练习册系列答案
相关题目
 一副三角板按如图方式摆放,如果∠2=18°,则∠1=( )
一副三角板按如图方式摆放,如果∠2=18°,则∠1=( )| A、18° | B、54° |
| C、72° | D、70° |
 如图,把边长为5cm的正方形ABCD先向右平移a cm,再向上平移b cm(a、b均小于5),得到正方形EFGH,阴影部分的面积为
如图,把边长为5cm的正方形ABCD先向右平移a cm,再向上平移b cm(a、b均小于5),得到正方形EFGH,阴影部分的面积为 已知:点A(3,4),B(-2,3),C(1,0)
已知:点A(3,4),B(-2,3),C(1,0) 如图所示,点E在AC上,∠1=∠2,∠3=∠4,试说明:BE=DE.
如图所示,点E在AC上,∠1=∠2,∠3=∠4,试说明:BE=DE. 我国体育健儿在24届-30届奥运会上获得金牌的情况如图所示,则在这七届奥运会上,我国体育健儿共获得
我国体育健儿在24届-30届奥运会上获得金牌的情况如图所示,则在这七届奥运会上,我国体育健儿共获得