题目内容
13.在Rt△ACB中,∠ABC=90°,BC=6cm,AC=10cm.
(1)求AB的长.
(2)若点P从点B出发,以2cm/s的速度在BC所在的直线l上运动,设运动时间为t,那么当t为何值时,△ACP为等腰三角形?
分析 (1)直接利用勾股定理计算AB长即可;
(2)此题要分四种情况:当P向左移动时:分CA=PA,AP=PC,PC=AC三种情况,当P向右移动时,AC=CP分别计算出t的值即可.
解答 解:(1)∵∠ABC=90°,BC=6cm,AC=10cm,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{100-36}$=8(cm);
(2)如图所示: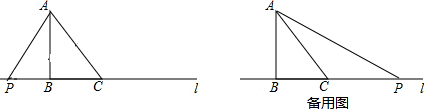 当P向左移动时,PB=2t,
当P向左移动时,PB=2t,
若AP=AC=10cm,
则:BP=$\sqrt{A{P}^{2}-A{B}^{2}}$=6(cm),
2t=6,
t=3;
若PC=AC=10cm,则BP=4cm,
2t=4,
解得:t=2;
若AP=PC,则PC=6+2t,AP=6+2t,
(2t)2+82=(6+2t)2,
解得:t=$\frac{7}{6}$,
当P向右移动时,BP=2t,则CP=2t-6,
当AC=CP时,2t-6=10,
解得:t=8.
答:当t为3,2,8huo$\frac{7}{6}$时,△ACP为等腰三角形.
点评 此题主要考查了勾股定理和等腰三角形的判定,关键是要分情况讨论,不要漏解.

练习册系列答案
相关题目
5.在平面直角坐标系中,点(2,3)关于y轴对称的点的坐标是( )
| A. | (-2,-3) | B. | (2,-3) | C. | (-2,3) | D. | (2,3) |
3. 如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
 如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )| A. | ∠ACD=120° | B. | ∠ACD=∠BCE | C. | ∠ACE=120° | D. | ∠ACE-∠BCD=120° |
 如图,直线CO⊥AB于点O,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的$\frac{1}{4}$.过点C作CE⊥AD,交AB交于F,垂足为E.
如图,直线CO⊥AB于点O,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的$\frac{1}{4}$.过点C作CE⊥AD,交AB交于F,垂足为E. 在4×6的方格中
在4×6的方格中 如图,在△ABC中,AB>AC,在边AB上,取点D,在AC上取点E,使AD=AE,直线DE和BC的延长线交于点P.
如图,在△ABC中,AB>AC,在边AB上,取点D,在AC上取点E,使AD=AE,直线DE和BC的延长线交于点P.