Question

18．如图，在△ABC中，AB＞AC，在边AB上，取点D，在AC上取点E，使AD=AE，直线DE和BC的延长线交于点P．
求证：BP•CE=BD•CP．

Answer 1

分析 如图，过点B作BF∥AC交PD延长线于点F．则△PCE∽△PBF，所以该相似三角形的对应边成比例，即$\frac{BF}{CE}=\frac{BP}{CP}$，根据平行线的性质，等腰三角形的性质以及对顶角的定义得BF=BD．则$\frac{BF}{CE}=\frac{BD}{CE}$，等量代换得到BP：CP=BD：CE，即可得到结论．

解答 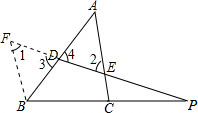证明：如图，过点B作BF∥AC交PD延长线于点F．则△PCE∽△PBF，
∴$\frac{BF}{CE}=\frac{BP}{CP}$，
∵BF∥AC，
∴∠1=∠2．
又∵AD=AE，
∴∠2=∠4，
∠1=∠3=∠4，
∴BF=BD．
∴$\frac{BF}{CE}=\frac{BD}{CE}$，
∴BP：CP=BD：CE，
∴BP•CE=BD•CP．

点评 本题考查了相似三角形的判定与性质．寻找相似三角形的一般方法是通过作平行线构造相似三角形．