题目内容
8. 在4×6的方格中
在4×6的方格中(1)画出与格点△ABC相似的△DEF(相似比不为1,且顶点应在格点上);
(2)证明你的结论.
分析 (1)把△ABC缩小$\frac{1}{2}$可画出△DEF;
(2)先计算出两个三角形的各边长,然后利用三组对应边的比相等的两三角形相似进行判断.
解答 解:(1)如图,△DEF为所作;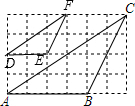
(2)证明如下:∵AB=4,BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,AC=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,DE=2,EF=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,DF=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∴$\frac{DE}{AB}$=$\frac{2}{4}$=$\frac{1}{2}$,$\frac{EF}{BC}$=$\frac{\sqrt{5}}{2\sqrt{5}}$=$\frac{1}{2}$,$\frac{DF}{AC}$=$\frac{\sqrt{13}}{2\sqrt{13}}$=$\frac{1}{2}$,
∴$\frac{DE}{AB}$=$\frac{EF}{BC}$=$\frac{DF}{AC}$,
∴△DEF∽△ABC.
点评 本题考查了作图-相似变换:两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.

练习册系列答案
相关题目
19.下列语句不是命题的是( )
| A. | 延长AB到D,使BD=$\frac{1}{3}$AB | B. | 两点之间线段最短 | ||
| C. | 两条直线相交有且只有一个交点 | D. | 等角的补角相等 |
17.以下说法正确的是( )
①一条直角边和斜边上的高对应相等的两个直角三角形全等;
②有两条边相等的两个直角三角形全等;
③有一边相等的两个等边三角形全等;
④两边和其中一边的对角对应相等的两个三角形全等.
①一条直角边和斜边上的高对应相等的两个直角三角形全等;
②有两条边相等的两个直角三角形全等;
③有一边相等的两个等边三角形全等;
④两边和其中一边的对角对应相等的两个三角形全等.
| A. | ①② | B. | ②④ | C. | ①③ | D. | ①③④ |
18.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:

(1)根据上面多面体的模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2;
(2)一个多面体的棱数比顶点数大10,且有12个面,则这个多面体的棱数是30;
(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成,每个顶点处都有3条棱,共有棱36条.若该多面体外表面三角形的个数比八边形的个数的2倍多2,求该多面体外表面三角形的个数.

(1)根据上面多面体的模型,完成表格中的空格:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
(2)一个多面体的棱数比顶点数大10,且有12个面,则这个多面体的棱数是30;
(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成,每个顶点处都有3条棱,共有棱36条.若该多面体外表面三角形的个数比八边形的个数的2倍多2,求该多面体外表面三角形的个数.
