题目内容
3. 如图,直线CO⊥AB于点O,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的$\frac{1}{4}$.过点C作CE⊥AD,交AB交于F,垂足为E.
如图,直线CO⊥AB于点O,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的$\frac{1}{4}$.过点C作CE⊥AD,交AB交于F,垂足为E.(1)求线段CE的长;
(2)连接GF.请你判断GF与CB的位置关系,并说明理由.
分析 (1)过D作DH垂直于AB,由OA=OB=OC,求出AB的长,进而求出三角形ABC面积,根据三角形ABC面积与三角形ABD面积的关系求出三角形ABD面积,进而求出DH的长,根据三角形BOC为等腰直角三角形,得到三角形BDH为等腰直角三角形,求出HB的长,由AB-HB求出AH的长,在直角三角形ADH中,利用勾股定理求出AD的长,由三角形ABC面积减去三角形ABD面积求出三角形ACD面积,即可确定出CE的长;
(2)连接GF,可得GF与BC平行,理由为:由一对对顶角相等,一对直角相等,利用内角和定理得到一对角相等,再由OA=OC,利用ASA得到三角形AOG与三角形COF全等,利用全等三角形对应边相等得到OG=OF,即三角形GOF为等腰直角三角形,进而得到一对同位角相等,利用同位角相等两直线平行即可得证.
解答 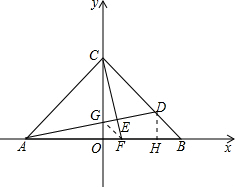 解:(1)过D作DH⊥AB,交AB于点H,
解:(1)过D作DH⊥AB,交AB于点H,
∵AO=OB=OC=8,即AB=16,且OC⊥AB,
∴△ABC面积为$\frac{1}{2}$AB•OC=64,
∵△ABD的面积为△ABC面积的$\frac{1}{4}$,
∴△ABD面积为$\frac{1}{2}$AB•DH=$\frac{1}{2}$×16DH=16,△ACD面积为64-16=48,
∴DH=2,
∵OB=OC,OC⊥OB,
∴△BOC为等腰直角三角形,即∠CBO=45°,
∴△DBH为等腰直角三角形,即HB=DH=2,
∴AH=AB-HB=16-2=14,
在Rt△ADH中,根据勾股定理得:AD=$\sqrt{A{H}^{2}+D{H}^{2}}$=10$\sqrt{2}$,
∵CE⊥AD,△ACD面积为48,
∴$\frac{1}{2}$AD•CE=48,即$\frac{1}{2}$×10$\sqrt{2}$CE=48,
解得:CE=$\frac{24\sqrt{2}}{5}$;
(2)连接GF,可得GF∥CB,理由为:
∵∠CGD=∠AGO,∠COF=∠AOG=90°,
∴∠OAG=∠OCF,
在△AOG和△COF中,
$\left\{\begin{array}{l}{∠OAG=∠OCF}\\{OA=OC}\\{∠AOG=∠COF}\end{array}\right.$,
∴△AOG≌△COF(ASA),
∴OG=OF,
∴△GOF为等腰直角三角形,
∴∠GF0=45°,
∵∠B=45°,即∠GFO=∠B,
∴GF∥CB.
点评 此题考查了一次函数综合题,涉及的知识有:等腰直角三角形的判定与性质,全等三角形的判定与性质,平行线的判定,以及三角形面积求法,熟练掌握全等三角形的判定与性质是解本题第二问的关键.

 全优点练单元计划系列答案
全优点练单元计划系列答案 如图,已知AB是⊙O的切线,点A为切点,连接OB交⊙O于点C,∠B=38°,点D是⊙O上一点,连接CD,AD.则∠D等于( )
如图,已知AB是⊙O的切线,点A为切点,连接OB交⊙O于点C,∠B=38°,点D是⊙O上一点,连接CD,AD.则∠D等于( )| A. | 76° | B. | 38° | C. | 30° | D. | 26° |
| A. | 相等 | B. | 都是0 | ||
| C. | 互为相反数 | D. | 相等或互为相反数 |
 已知二次函数的解析式是y=x2-2x-3
已知二次函数的解析式是y=x2-2x-3