题目内容
4.已知关于x的一元二次方程(m-1)x2+2mx+m+3=0(1)若方程有两个相等的实数根时,求m的值.
(2)当方程没有实数根时,求出m的最小正整数的值.
分析 (1)根据一元二次方程的定义和判别式的意义得到m-1≠0且△=4m2-4(m-1)(m+3)=0,然后解关于m的一次方程即可;
(2)根据一元二次方程的定义和判别式的意义得到m-1≠0且△=4m2-4(m-1)(m+3)<0,然后解两个不等式得到m的取值范围,再在此范围内找出最小正整数即可.
解答 解:(1)根据题意得m-1≠0且△=4m2-4(m-1)(m+3)=0,
所以m=$\frac{3}{2}$;
(2)根据题意得m-1≠0且△=4m2-4(m-1)(m+3)<0,
所以m>$\frac{3}{2}$,
所以m的最小正整数的值为2.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
14.如果两个数的绝对值相等,那么这两个数( )
| A. | 相等 | B. | 都是0 | ||
| C. | 互为相反数 | D. | 相等或互为相反数 |
19.下列语句不是命题的是( )
| A. | 延长AB到D,使BD=$\frac{1}{3}$AB | B. | 两点之间线段最短 | ||
| C. | 两条直线相交有且只有一个交点 | D. | 等角的补角相等 |
9.下列计算正确的是( )
| A. | 23=6 | B. | (-3)2=-9 | C. | (-2)3=-8 | D. | -42=16 |
 已知二次函数的解析式是y=x2-2x-3
已知二次函数的解析式是y=x2-2x-3
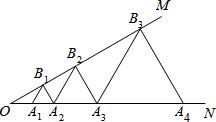 如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4 …均为等边三角形,若OA1=$\frac{1}{3}$,则△A2015B2015A2016的边长为$\frac{{2}^{2014}}{3}$.
如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4 …均为等边三角形,若OA1=$\frac{1}{3}$,则△A2015B2015A2016的边长为$\frac{{2}^{2014}}{3}$.