题目内容
17.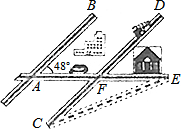 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )| A. | 48° | B. | 40° | C. | 30° | D. | 24° |
分析 先根据平行线的性质,由AB∥CD得到∠1=∠BAE=45°,然后根据三角形外角性质计算∠C的度数.
解答  解:∵AB∥CD,
解:∵AB∥CD,
∴∠1=∠BAE=48°,
∵∠1=∠C+∠E,
∵CF=EF,
∴∠C=∠E,
∴∠C=$\frac{1}{2}$∠1=$\frac{1}{2}$×48°=24°.
故选D.
点评 本题考查了等腰三角形的性质,平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
8.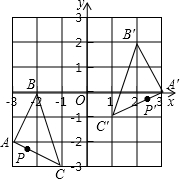 如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )
如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )
 如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )
如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )| A. | (-m,n+2) | B. | (-m,n-2) | C. | (-m-2,-n) | D. | (-m-2,n-2) |
12.化化工产品C是由A,B两种原料加工而成的,每个C产品的质量为50kg,经测定加工费与A的质量的平方成正比例;A原料的成本10元/kg,B原料的成本:40元/kg;这种C产品中A的含量不能低于10%,又不能高于60%;C产品的出厂价经核算是含B的质量的一次函数.经市场调查,当含A的质量不高于8kg时:利润=出厂价-成本;当含A的质量不低于8kg时,每个C产品的利润将与含A的质量成反比例.
下表是每个C产品的成本及出厂价一览表的一部分.
(1)求出每个C产品的成本y(元)与含A的质量x(kg)之间的函数关系式,并写出x的范围;(每个C成本=A的成本+B的成本+加工费用);
(2)求出每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式.
下表是每个C产品的成本及出厂价一览表的一部分.
| 含A:10% | 含A(30%) | |
| 成本(元/个) | 1875 | 1775 |
| 出厂价 | 2450 | 2350 |
(2)求出每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式.
9.下列运算正确的是( )
| A. | $\frac{3a+b}{6}$=$\frac{a+b}{2}$ | B. | 2×$\frac{a+b}{3}$=$\frac{2a+b}{3}$ | C. | $\sqrt{{a}^{2}}$=a | D. | |a|=a(a≥0) |
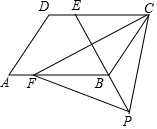 如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:
如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论: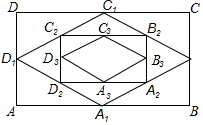 由四边形四条边的中点组成的四边形叫做原四边形的中点四边形.如图,四边形ABCD是矩形,取矩形ABCD四条边的中点得到中点四边形A1B1C1D1,再取四边形A1B1C1D1四条边的中点得到中点四边形A2B2C2D2,…,按此规律继续下去,若矩形ABCD的面积为1,则得到的中点四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$.
由四边形四条边的中点组成的四边形叫做原四边形的中点四边形.如图,四边形ABCD是矩形,取矩形ABCD四条边的中点得到中点四边形A1B1C1D1,再取四边形A1B1C1D1四条边的中点得到中点四边形A2B2C2D2,…,按此规律继续下去,若矩形ABCD的面积为1,则得到的中点四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$.