题目内容
20.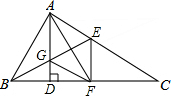 如图所示,在△ABC中,∠BAC=90°,AD⊥BC,BE,AF分别是∠ABC,∠DAC的平分线,BE和AD交于G,试说明四边形AGFE的形状.
如图所示,在△ABC中,∠BAC=90°,AD⊥BC,BE,AF分别是∠ABC,∠DAC的平分线,BE和AD交于G,试说明四边形AGFE的形状.
分析 首先证明∠ABC=∠DAC,∠BAD=∠C,再根据角平分线的性质证明∠ABG=∠EBD,然后可证出∠AGE=∠AEG,根据等角对等边可得AG=AE,再证明四边形AGFE是平行四边形,可根据一组邻边相等的平行四边形是菱形得到结论.
解答 解:四边形AGFE是菱形,
∵∠BAC=90°,AD⊥BC.
∴∠C+∠ABC=90°,∠C+∠DAC=90°,∠ABC+∠BAD=90°.
∴∠ABC=∠DAC,∠BAD=∠C.
∵BE、AF分别是∠ABC、∠DAC的平分线.
∴∠ABG=∠EBD.
∵∠AGE=∠GAB+∠GBA,∠AEG=∠C+∠EBD,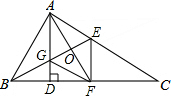
∴∠AGE=∠AEG,
∴AG=AE,
∵AF是∠DAC的平分线,
∴AO⊥BE,GO=EO,
∵在△ABO和△FBO中$\left\{\begin{array}{l}{∠ABO=∠FBO}\\{BO=OB}\\{∠AOB=∠FOB=90°}\end{array}\right.$,
∴△ABO≌△FBO(ASA),
∴AO=FO,
∴四边形AGFE是平行四边形,
又∵AG=AE,
∴四边形AGFE是菱形.
点评 此题主要考查了菱形的判定,关键是掌握一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
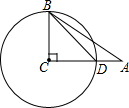 如图,在△ABC中,已知∠C=90°,sinA=$\frac{3}{5}$,以BC为半径的⊙C交AC边上一点D,若AD=4,求半径BC的长.
如图,在△ABC中,已知∠C=90°,sinA=$\frac{3}{5}$,以BC为半径的⊙C交AC边上一点D,若AD=4,求半径BC的长. 如图2、图3,AB∥EF,∠D与∠B,∠EFD有何数量关系?
如图2、图3,AB∥EF,∠D与∠B,∠EFD有何数量关系?