题目内容
15.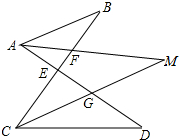 如图,AM是∠BAD的平分线,CM是∠BCD的平分线,AM、CM交于点M,CB、AM交于点F,AD、CM交于点G,AD、CB交于点E,∠B=32°,∠D=38°.
如图,AM是∠BAD的平分线,CM是∠BCD的平分线,AM、CM交于点M,CB、AM交于点F,AD、CM交于点G,AD、CB交于点E,∠B=32°,∠D=38°.(1)求∠M的度数;
(2)求∠B,∠M,∠D之间的关系.
分析 (1)根据三角形内角和定理用∠B、∠M表示出∠BAM-∠BCM,再用∠B、∠M表示出∠MAD-∠MCD,再根据角平分线的定义可得∠BAM-∠BCM=∠MAD-∠MCD,然后求出∠M与∠B、∠D关系,代入数据进行计算即可得解;
(2)根据三角形内角和定理用∠B、∠M表示出∠BAM-∠BCM,再用∠B、∠M表示出∠MAD-∠MCD,再根据角平分线的定义可得∠BAM-∠BCM=∠MAD-∠MCD,然后求出∠M与∠B、∠D关系.
解答 解:(1)解:根据三角形内角和定理,∠B+∠BAM=∠M+∠BCM,
∴∠BAM-∠BCM=∠M-∠B,
同理,∠MAD-∠MCD=∠D-∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M-∠B=∠D-∠M,
∴∠M=$\frac{1}{2}$(∠B+∠D)=$\frac{1}{2}$(32°+38°)=35゜;
(2)证明:根据三角形内角和定理,∠B+∠BAM=∠M+∠BCM,
∴∠BAM-∠BCM=∠M-∠B,
同理,∠MAD-∠MCD=∠D-∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M-∠B=∠D-∠M
∴2∠M与∠B+∠D.
点评 本题考查了三角形的内角和定理,角平分线的定义.注意利用对顶角相等和三角形外角的性质求出角的关系是解题的关键,要注意整体思想的利用.

练习册系列答案
相关题目
5.下列图形中,①正方形,②长方形,③等边三角形,④线段⑤角,绕某个点旋转180°能与自身重合的有( )
| A. | 5个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.我们学习了圆周角定理,回顾学习过程,在探索同弧所对的圆周角和圆心角的关系时,主要体现的数学思想是( )
| A. | 转化 | B. | 数形结合 | C. | 演绎 | D. | 分类讨论 |
 如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GDM:S△GAB的值为1:4.
如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GDM:S△GAB的值为1:4.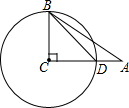 如图,在△ABC中,已知∠C=90°,sinA=$\frac{3}{5}$,以BC为半径的⊙C交AC边上一点D,若AD=4,求半径BC的长.
如图,在△ABC中,已知∠C=90°,sinA=$\frac{3}{5}$,以BC为半径的⊙C交AC边上一点D,若AD=4,求半径BC的长. 如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转过的总齿数是相同的,尝试回答下面问题.
如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转过的总齿数是相同的,尝试回答下面问题.